
 Jak to się nie przyda...
Jak to się nie przyda...  Liczysz wybraną parę przeciwległych kątów, czyli:
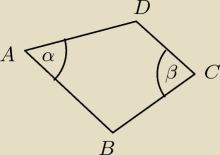
0. Wybieramy punkty, których kąty będziemy liczyć (np. A i C).
1. Liczymy wektory i ich długości.
AB→ = (−3−7, −3+3) = (−10, 0) ||AB→|| = 10
AD→ = (5−7, −7+3) = (−2, −4) ||AD→|| = √4+16 = 2√5
CD→ = (5+2, −7+6) = (7, −1) ||CD→|| = √49+1 = 5√2
CB→ = (−3+2, −3+6) = (−1, 3) ||CB→|| = √1+9 = √10
2. Liczymy iloczyny wektorowe.
Liczysz wybraną parę przeciwległych kątów, czyli:
0. Wybieramy punkty, których kąty będziemy liczyć (np. A i C).
1. Liczymy wektory i ich długości.
AB→ = (−3−7, −3+3) = (−10, 0) ||AB→|| = 10
AD→ = (5−7, −7+3) = (−2, −4) ||AD→|| = √4+16 = 2√5
CD→ = (5+2, −7+6) = (7, −1) ||CD→|| = √49+1 = 5√2
CB→ = (−3+2, −3+6) = (−1, 3) ||CB→|| = √1+9 = √10
2. Liczymy iloczyny wektorowe.
| 1 | ||
AB→oAD→ = 20 = 10*2√5*cosα → cosα = | . | |
| √5 |
| 1 | ||
CD→oCB→ = −7 −3 = −10 = 5√2*√10*cosβ → cosβ = − | . | |
| √5 |
| 1 | 1 | |||
cosα = | ⇒ α = arccos | |||
| √5 | √5 |
| 1 | 1 | 1 | ||||
cosβ = − | ⇒ β = arccos(− | ) = π − arccos | ||||
| √5 | √5 | √5 |
| 1 | 1 | |||
α+β = arccos | + π − arccos | = π. | ||
| √5 | √5 |
 A teraz niech ktoś to zrobi prościej.
A teraz niech ktoś to zrobi prościej. 
