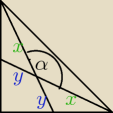
 W trójkącie prostokątnym równoramiennym poprowadzono środkowe z wierzchołków kątów ostrych.
Oblicz cos kąta rozwartego zawartego między nimi.
Wiem że środkowe dzielą się w stosunku 2:1. Przypuszczam że należy skorzystać z twierdzenia
cosinusów. Tylko jak to dobrze zrobić?
Proszę o jakieś wskazówki.
Pozdrawiam
W trójkącie prostokątnym równoramiennym poprowadzono środkowe z wierzchołków kątów ostrych.
Oblicz cos kąta rozwartego zawartego między nimi.
Wiem że środkowe dzielą się w stosunku 2:1. Przypuszczam że należy skorzystać z twierdzenia
cosinusów. Tylko jak to dobrze zrobić?
Proszę o jakieś wskazówki.
Pozdrawiam
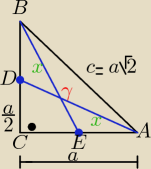 |AD|=|EB|=s−−− dł. środkowych
z ΔCAD z tw. Pitagorasa
s2= a2+(a2)2
|AD|=|EB|=s−−− dł. środkowych
z ΔCAD z tw. Pitagorasa
s2= a2+(a2)2
| 5a2 | ||
s2= | ||
| 4 |
| a√5 | ||
s= | ||
| 2 |
| 2 | ||
x= | s =.........
| |
| 3 |
| x2+x2− c2 | ||
cosγ= | =......... | |
| 2x*x*c |
 Oczywista oczywistość.
Eh.. Matma rozszerzona to chyba nie był najlepszy pomysł...
Oczywista oczywistość.
Eh.. Matma rozszerzona to chyba nie był najlepszy pomysł...
