ostro słup
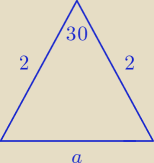
ICSP: Ściana boczna ostrosłupa prawidłowego trójkątnego jest trójkątem równoramiennym, w którym
ramiona mają długość 2 i kąt miedzy nimi ma 30 stopni. Oblicz pole powierzchni całkowitej.
Pole boczne policzę, ale nie mam pomysłu jak dojść do pola podstawy.
13 lut 19:01
Godzio:
Z tw. cosinusów policz a
Tyle

13 lut 19:04
ICSP: Problem w tym że jeszcze nie powtarzałem tw cosinusów. Jako że jestem z podstawy to nie mam
tego w programie. Mógłbyś to chociaż przybliżyć troszeczkę?
13 lut 19:05
Godzio:
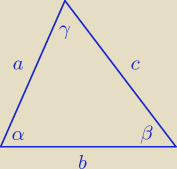
W dowolnym trójkącie zachodzi taka zależność:
a
2 + b
2 − 2abcosα = c
2
b
2 + c
2 − 2bccosβ = a
2
a
2 + c
2 − 2accosγ = b
2
13 lut 19:07
ICSP: podstawa mi wychodzi √8−4√3. Dobrze to jest?
13 lut 19:10
Godzio:
| | √3 | |
a2 = 4 + 4 − 2 * 2 * |
| |
| | 2 | |
a
2 = 8 − 2
√3
a =
√8 − 2√3
13 lut 19:12
ICSP: To przemnażam przez jeden bok czy przez dwa?
13 lut 19:14
Godzio:
Ale co przemnażasz ?
13 lut 19:16
Eta:
Godzio
| | √3 | |
a2= 4+4−2*2*2* |
| = ........... 
|
| | 2 | |
Do pola podstawy potrzebne jest
a2
a
2= 8−4
√3
13 lut 19:17
ICSP: To po minusie. tam jest 2 * a * b * cosγ.
13 lut 19:17
ICSP: Dziękuje wam za pomoc

. Zostały jeszcze tylko dwa zadanka

13 lut 19:18
Godzio: aa

2 zjadłem
13 lut 19:19
Eta:
Wielka szkoda,że tylko dwa

13 lut 19:19
ICSP: Może i szkoda. Ja już mam na dzisiaj dość. Mam jeszcze takie pytanie. Jeżeli trójkąt jest
równoramienny to do twierdzenia cosinusów wystarczy podstawa tego trójkąta i kąt miedzy
ramionami jako dane aby obliczyć pozostałe dwa boki?
13 lut 19:21
13 lut 19:21
Godzio:
ICSP tak

Dzięki
Eta ale owoców już mam na dzisiaj dość

13 lut 19:22
13 lut 19:24
Godzio:
Hahaha

Nie da się zapomnieć
13 lut 19:25
Eta:

13 lut 19:26
ICSP: Padłem na ostatnim:(
Dany jest ostrosłup prawidłowy czworokątny o podstawie ABCD i wierzchołku S. Punkt P jest
środkiem odcinka As. Wyznacz cosinusy kątów trójkąta ACP, jeśli krawędź boczna ostrosłupa jest
równa krawędzi podstawy.
13 lut 19:31
Godzio:
Uwielbiam takie zadania, nic nie jest dane i trzeba coś obliczyć, najfajniejsze zadania

13 lut 19:32
Godzio:
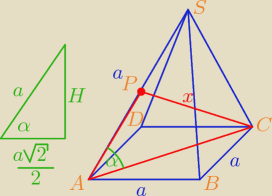
|AB| = a
|AC| = a
√2
|PC| = x
Z tw. cosinusów w trójkącie ACP :
| | a | | a | |
( |
| )2 + (a√2)2 − 2 * |
| * a√2 * cosα = x2 |
| | 2 | | 2 | |
Wylicz z tego x i cosinusy pozostałych kątów wyliczysz już z tego twierdzenia
13 lut 19:39
13 lut 19:57
Godzio:
Tak
13 lut 19:59
ICSP: Jest w końcu powychodziło. Dzięki wielki godziu


. Tobie również eta


.
13 lut 20:08
 Z tw. cosinusów policz a
Z tw. cosinusów policz a

 W dowolnym trójkącie zachodzi taka zależność:
a2 + b2 − 2abcosα = c2
b2 + c2 − 2bccosβ = a2
a2 + c2 − 2accosγ = b2
W dowolnym trójkącie zachodzi taka zależność:
a2 + b2 − 2abcosα = c2
b2 + c2 − 2bccosβ = a2
a2 + c2 − 2accosγ = b2


 . Zostały jeszcze tylko dwa zadanka
. Zostały jeszcze tylko dwa zadanka
 2 zjadłem
2 zjadłem










 Dzięki Eta ale owoców już mam na dzisiaj dość
Dzięki Eta ale owoców już mam na dzisiaj dość 



 ( jak Kamil ... pamiętasz?
( jak Kamil ... pamiętasz? 
 Nie da się zapomnieć
Nie da się zapomnieć


 |AB| = a
|AC| = a√2
|AB| = a
|AC| = a√2

 . Tobie również eta
. Tobie również eta

 .
.