badanie przebiegu funkcji
Marta: Witam potrzebuje pomocy ze znalezieniem ekstremum lokalnego i przedziałów monotoniczności
| | ln2x | |
funkcji y= |
| . Z góry dziękuje za pomoc  |
| | x | |
13 lut 17:32
Marta: czy ekstremum bedzie w puknice (1,0), a liczy sie to z pierwszej pochodnej przyrownanej do
zera?
Czy funkcja maleje dla x∊(0,1) a rosnie dla x∊(1,+∞)?
13 lut 17:45
Marta: 1
x +∞ ↘ min ↗ +∞
−−−−−−−−−−o−−−−−−−−−−−−−−−−−−−−−−−−−−o−−−−−−−−−−−−−−−−−−−−−−−−−−−−>
f(x) 0 1 +∞
Czy dobrze to rozwiązałam?
13 lut 18:14
Marta: ups troche sie przesunelo

13 lut 18:15
Marta: tzn os sie przesunela

punkty sa w 0 i 1
13 lut 18:15
Marta: ktos oceni?
13 lut 19:25
Marta: prosze?
13 lut 19:59
Godzio:
Zaraz sprawdzę
13 lut 20:03
Godzio:
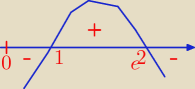
D = (0,
∞)
f'(x) > 0
lnx(2 − lnx) > 0
0 < lnx < 2
1 < x < e
2
f ↗ (1,e
2)
f↘ (0,1) , (e
2,
∞)
f(1) = 0
| | 4 | |
Maksimum lokalne: (e2, |
| ) |
| | e2 | |
Minimum lokalne: (1,0)
13 lut 20:17
Marta: dlaczego pochodna z ln2x = lnx−ln2x?
13 lut 20:23
Godzio:
| | 1 | |
Pochodna z In2x to 2Inx * |
| |
| | x | |
13 lut 20:24
Marta: prosilabym o rozpisanie

13 lut 20:24
Marta: aha dziekuje bardzo

13 lut 20:24
Godzio:
| | ln2x | | (ln2x) * x − (x)' * ln2x | | | | 1 | | 2lnx * |
| * x − 1 * ln2x | | | x | |
| |
( |
| )' = |
| = |
| = |
| | x | | x2 | | x2 | |
13 lut 20:25
Marta: | | 2lnx | |
skoro ln2x= |
| to jak obliczyes ta pochodna  |
| | x | |
13 lut 20:27
Marta: aaaa przepraszam bardzo z granicami juz mi sie myli
13 lut 20:27
Godzio:

13 lut 20:28
Marta: lne2 = 4? a nie 2?
13 lut 20:42
Marta: kwadrat zgubilam

ide chyba lepiej spac bo nie mysle juz
13 lut 20:47
Godzio: 
13 lut 20:52


 punkty sa w 0 i 1
punkty sa w 0 i 1





 ide chyba lepiej spac bo nie mysle juz
ide chyba lepiej spac bo nie mysle juz
