kąty wpisane i środkowe 1ADA: Na przedłużeniu cięciwy AB danego okręgu poza punkt B wybieramy punkt C, w odleglości od punktu B równej długości promienia okręgu. przez punkt C prowadzimy prostą przechodzącą przez środek O okręgu i literą D oznaczamy jeden z punktów przecięcia tej prostej z okręgiem tak, żeby środek O leżał między punktami C i D. udowodnij, że miara kąta AOD jest trzy razy większa od miary kąta BOC. Dzziękuje z gory za pomoc

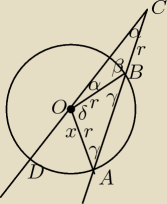
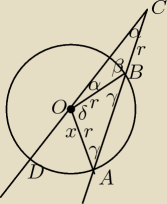sonia: Należy zauważyć, że ΔAOB i ΔOBC są równoramienne, więc kąty przy podstawach tych trójkątów mają równe miary. β =180−2α (suma miar kątów w trójkącie jest równa 180) γ=180−β=180−(180−2α)=180−180+2α=2α δ=180−2γ=180−2*2α=180−4α x+δ+α=180 x+180−4α+α=180 x−3α=0 x=3α cnd