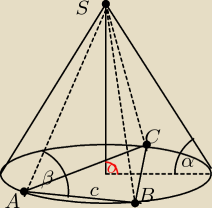
 W stożek, którego tworząca jest nachylona do podstawy pod kątem α, wpisano ostrosłup SABC,
którego podstawą jest trójkąt równoramienny △ABC. W trójkącie tym |AC|=|BC|, zaś |AB|=c. Kąt
między krawędziami SA i AB jest równy β. Oblicz pole powierzchni całkowitej stożka.
W stożek, którego tworząca jest nachylona do podstawy pod kątem α, wpisano ostrosłup SABC,
którego podstawą jest trójkąt równoramienny △ABC. W trójkącie tym |AC|=|BC|, zaś |AB|=c. Kąt
między krawędziami SA i AB jest równy β. Oblicz pole powierzchni całkowitej stożka.

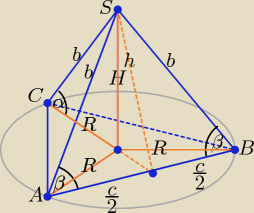 b − tworzącą stożka i krawędź boczna ostrosłupa.
Pole powierzchni bocznej stożka P = πR2 + πRb
b − tworzącą stożka i krawędź boczna ostrosłupa.
Pole powierzchni bocznej stożka P = πR2 + πRb
| c | |||||||||||
= cosβ ⇒ b = | , | |||||||||||
| b | 2cosβ |
| R | c*cosα | ||
= cosα ⇒ R = b*cosα = | , | ||
| b | 2cosβ |

