Nie mam pomysłu

Nie mam pomysłu basiulek: Oblicz długość promienia okręgu wpisanego w trapez równoramienny , w którym iloczyn długości podstaw jest równy 64

9 lut 20:21

basiulek: Cz ma ktos pomysł?

9 lut 20:33

basiulek: ICSP pomóż

9 lut 20:39

Tragos: ab = 64 a + b = 2c ( zgodnie z https://matematykaszkolna.pl/strona/874.html ) r = 2h zrób sobie rysunek, może na coś wpadniesz emotka

9 lut 20:53

basiulek: Tragos nie mam pojęcia emotka

9 lut 20:57

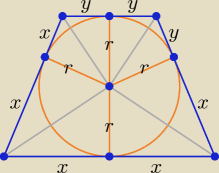
Bogdan: rysunek

x > 0, y > 0, r > 0 2x * 2y = 64 ⇒ xy = 16 r² = x*y ⇒ r² = 16 ⇒ r = 4

9 lut 21:11

basiulek: Dlaczego r² = x * y ?

9 lut 21:21

basiulek: Boguś nie mam pojęcia ? Pomożesz?

9 lut 21:31

Bogdan: Tak od razu, bez żadnego wysiłku ze swojej strony chcesz wiedzieć? Uruchom szare komórki emotka

9 lut 21:34

basiulek: kombinuję please

mała podpowiedź

9 lut 21:38

Bogdan: Czasami trzeba kombinować kilka godzin, a nawet dni emotka

9 lut 21:40

basiulek: Potrzebne mi to na jutro

9 lut 21:41

ICSP: Tam na rysunku to ci chyba ten x się pomylił z y.

9 lut 21:43

basiulek: wiem że to pomyłka z tym x po lewej na górze. Widzę że są tam trójkąty przystające, ale nie wiem dla czego r²=x*y

9 lut 21:45

Bogdan: No, wreszcie ktoś zauważył emotka

9 lut 21:46

basiulek: Boguś proszę bo i mózg paruje emotka

9 lut 21:47

ICSP: bok = x+y "częśc" podstawy jeżeli przesunę ten odcinek 2r o y jednostek będzie równe x − y (x−y)² + 4r² = (x+y)² ⇔ x² − 2xy + y² + 4r² = x² + 2xy + y².

9 lut 21:48

Bogdan: Poszukaj trójkątów podobnych

9 lut 21:51

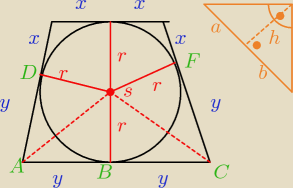
TOmek: rysunek

wiemy ,ze x*y=16 wiem ,ze jest takie "twierdzenie" (pomaranczowy rysunek) h=√a*b tylko nie wiem jak to tutaj wprowadzić ..

9 lut 22:00

basiulek: Dzieki chłapaki. jesteście Kochani

9 lut 22:01

basiulek: ICSP zrobiła z Tw. Pitagorasa a Bogdan z trójątów podobych , ułozył proporcję z bokami.

9 lut 22:03

TOmek: ja nadal nie wiem jak to zrobic

9 lut 22:06

basiulek: emotka

A ja wiem i to dwa sposoby zrozumiałam

9 lut 22:07

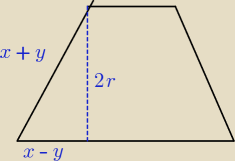
TOmek: rysunek

(x−y)²+(x+y)²=4r i co dalej?

9 lut 22:09

TOmek: to teraz mi pomoz

9 lut 22:09

basiulek: Ta proporcja to ^x_r = ^r_y

9 lut 22:11

basiulek: a tu zastosuj wzory skróconego mnożenia

9 lut 22:12

TOmek: no to czaje, ale jeszcze na trójkąty podobne nie łapie..

9 lut 22:13

TOmek: potrafisz pokazac które trójkąty są podobne i skąd to wziąłes?

9 lut 22:14

basiulek: Mały trójkąt i duży maja takie same katy

9 lut 22:16

TOmek: aha,,czaje ;0

9 lut 22:19

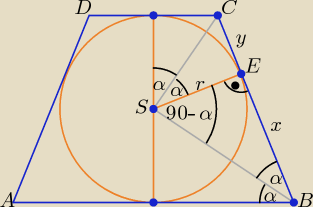
Bogdan: rysunek

Punkt S jest punktem przecięcia dwusiecznych kątów wewnętrznych trapezu. Trójkąty BES i CES są podobne, ponieważ mają równe kąty wewnętrzne.

y		r
	=		⇒ r² = xy
r		x

9 lut 22:20

basiulek:

sama na to wpadłam

9 lut 22:23

Bogdan: I na to liczyłem basiulek, że dasz radę emotka

9 lut 22:25

;): h²=|CE|*|BE|

9 lut 23:03