matematykaszkolna.pl
Zbadać monotoniczność, znaleźć ekstrema oraz naszkicować wykres ! Szym: f(x)= − xlnx
8 lut 23:31
Jack: licz pochodną na początek.
8 lut 23:43
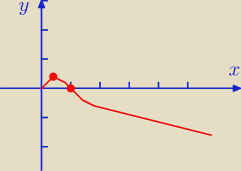
Godzio: rysunek D = (0,∞) f(x) = − xlnx f(x) = 0 ⇔ x = 1
 1 
f'(x) = − lnx − x *
= −lnx − 1
 x 
 1 1 1 
f'(x) = 0 ⇒ −lnx − 1 = 0 ⇒ lnx = − 1 ⇒ x =
, f(
) =
 e e e 
 1 1 
f'(x) > 0 ⇒ lnx < − 1 ⇒ x <
, f'(x) < 0 ⇒ x >
 e e 
 1 
f ↗ (0,
)
 e 
 1 
f ↘ (
,∞)
 e 
 1 1 
Maksimum lokalne: (
,
)
 e e 
8 lut 23:46
Szym:
 1 −1 
f'(x)= −1*
=
 x x 
 −1 
f''(x)=
 x2 
Przedziały monotoniczności:
−1 
>0
x 
x(−1)>0 x>1 dobrze to jest? co dalej mam robić?
8 lut 23:57
Szym:
 1 
NIe ogarniam skąd to
mógłby mnie ktoś oświecić?
 e 
9 lut 00:02
Godzio:
 1 
Inx = logex = − 1 ⇔ e−1 = x ⇒ x =
 e 
9 lut 00:06
Szym: Wielkie dzięki za pomoc !
9 lut 00:23