Ostrokątny tójkąt ramiennny... rudy102333: Ostrokątny trójkąt równoramienny ABC o podstawie AB jest wpisany w okrąg o środku S, przy czym kąt SAB ma miarę 40 D .Oblicz miarę kąta CAB rysunek mam wykonany wiec tylko obliczenia mi trzeba lub powiedziec z czego skozystac thx za kazdą pomoc

rudy102333: bo mysle ze to jest tak SZUKANE: KAT ABC= α DANE: kąt SAB=40 WIEC kąt ABS=40 ABS= β i SAB=β (gdyz trójkąt jest równoramienny) wiec kąt ABC=2* kąt ABS dyz dwusieczna dzieli katy na połowy Kąt ABC=2*40 kąt ABC=80 DOBRZE ROZWIĄZANE

rudy102333: nikt nie sprawdzi ?

Gareth07: jak dla mnie źle , moim zdaniem: kąt SAB = 40 gdy narysujemy sobie rysunek, powstanie nam trójkąt ABS , gdzie dwa jego boki mają po 40, a więc kąt ASB : 180 − 2*40 = 100 , a wiec z def : kąt środkowy jest 2x wiekszy od kąta wpisanego opartym na tym samym łuku co kąt srodkowy , daje nam że kąt ACB = 50 a więc mozna ozaczyć nasz szukany kąt CAB jako 1/2α + 40 50+40+40 = 180 130 = 180 α=180−130 α=50 1/2α = 25 CAB = 25 + 40 CAB = 65

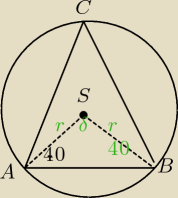
Mila: ΔABC jest ostrokątny δ=180−(40+40)=100 ∡ACB=50 jako wpisany oparty na tym samym łuku, co środkowy o mierze 100⁰. 180−50=130 ∡CAB=∡CBA=(130:2)=65⁰.

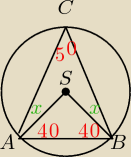
krystek: [180−(130)]:2=x⇒x=25