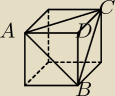
Stereometria. calineczka: Z sześcianu wycięto ostrosłup ABCD. Stosunek objętości sześcianu do objętości powstałej bryły jest równy:

Mendoza: V₁ − Objętość sześcianu V₂ − Obj. czworościanu. Z rysunku wynika, że ma wszystkie krawędzie równe więc jest to czworościan foremny. V₁ = a³

	a3√2
V2 =
	12

	V1		12		12
Stosunek:		= a3 *		=
	V2		a3√3		√3

12		√3		12√3		12√3
	*		=		=		= 4√3
√3		√3		√3 * √3		3

V1
	= 4√3
V2

Basia: to nie jest czworościan foremny; trzy krawędzie = krawędzie sześcianu trzy pozostałe = przekątnym ścian sześcianu

calineczka: Odpowiedzi do zadania są takie: A) 6:1 B) 5:1 C) 4:1 D) 3:1

Mendoza: Teraz dobrze: V₁ = a³

	1
V2 =		Pp * h
	3

h=a

	a2
Pp =
	2

	1		a2		a3
V2 =		*		{a} =
	3		2		6

V1		6		6
	= a3 *		=		= 6:1
V2		a3		1

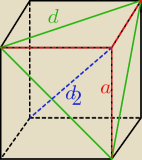
calineczka: Dziękuje Do tego samego rysunku jest to zadanie: Jeżeli długość boku sześcianu jest równa a, to pole powierzchni całkowitej ostrosłupa ABCD wynosi: A) a² B) ^a2√3₂ C) ^3a2₂ D) ^a2(3+√3)₂

calineczka: ?

Mendoza:

Mendoza:

	d2√3
Pole na Δ równoramienny: P =
	4

P = P_b d = a√2 P_c = 3P_p + P_b

	a2
Pp =
	2

	3a2		d2√3		3a2		2a2√3
Pc =		+		=		+
	2		4		2		4

	3a2		a2√3
Pc =		+
	2		2

	a2(3 + √3)
Pc =
	2

Aga1.: Np. Trójkąt ABD to połowa kwadratu ( przekątna AB dzieli ścianę boczną na dwa przystające trójkąty ) P_kwadratu=a² Pole trójkąta, to połowa pola kwadratu

	1
stąd Pp=		a2
	2

no name: Z kąd Ci się wzieło h=a? i jakim cudem pole podstawy wyszło Ci a²/2?