zad krucz: Dany jest ostrosłup prawidłowy trójkatny o krawędziach bocznych trzy razy dłuższych od krawędzi podstawy. Oblicz stosunek wysokości ostrosłupa do krawędzi jego podstawy.

krucz: Pomoże ktoś?

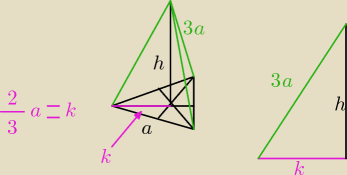
Mendoza: Ze wzoru Pitagorasa: (3a)² = k² + h²

	(2a)2
9a2 =		+ h2
	32

	4a2
9a2 =		+ h2
	9

	4a2
9a2 −		= h2
	9

	77a2
h2 =
	9

	a√77
h=
	3

a√77		a√77		1		√77
	: a =		*		=
3		3		a		3

Eta: @Mendoza

	a√3
k =
	3

zatem popraw swoje obliczenia

Mendoza: FUCK! . . . . . . . . . . . . . . . . . .

Mendoza: Jadę od początku: h₁ − wysokość trójkąta równobocznego h − wysokość ostrosłupa prawidłowego a − długość krawędzi podstawy 3a − długość krawędzi bocznej ostrosłupa k − dwie trzecie długości środkowej h₁. k = ²₃h₁ wzór na stronie 495

	a√3
h1 =
	2

	2		a√3		a√3
k =		*		=
	3		2		3

Pitagoras: a² + b² = c² k² + h² = (3a)²

	3a2		3a2
		+ h2 = 9a2 / −
	9		9

	a2
h2 = 9a2 −
	3

	27a2 − a2
h2 =
	3

	√26a		√3		√78a
h =		*		=
	√3		√3		3

	h		√78a		1		√78
		=		*		=
	a		3		a		3