tryg tryg: rozwiaz nierownosc dla x∊<−π,π>

	π
|cosx|(cosx−cos		)≥0
	4

tryg:

Godzio: Poszukaj tego zadania, już z 10 razy było rozwiązywane

Godzio: Taki początek:

	π
cosx = 0 lub cosx > cos
	4

dlaczego ? spróbuj sobie odpowiedzieć

tryg: zrobi ktos?

tryg: nie znalazlem

tryg: wiec?

Godzio: napisałem co musisz rozwiązać, zastanawiałeś się dlaczego tak ?

tryg: cosx=0 no bo beda dwa przypadki i co dalej?

Godzio: i musisz rozwiązać tą nierówność, suma rozwiązań z niej + cosx = 0 da Ci odpowiedź

tryg: cosx=0 + rozw cosx=0 to sa rozw −.− pomoze ktos?

tryg: cosx(cosx−√2{2})≥0 cosx=0 u cosx=√2{2}

	π
x=		+kπ
	2

	π
x=		+2kπ
	4

	7π
x=		+2kπ
	4

i nie wiem co dalej

Godzio: Dobra, zaraz pokaże jak

Godzio:

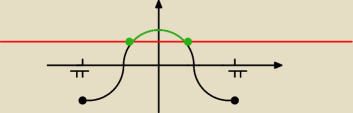
	π
|cosx| * (cosx − cos		) ≥ 0 x ∊ <−π,π>
	4

|cosx| jest zawsze większy lub równy 0, kiedy jest równy 0 to wpływa nam na rozwiązanie

	π
cosx = 0 ⇒ x =		+ kπ k ∊ C
	2

Żeby nierówność była spełniona musi zachodzić:

	π		π		π		π
cosx ≥ cos		⇒ cosx = cos		⇒ x =		lub x = −
	4		4		4		4

	π		π
x ∊ <		,−		>
	4		4

	π		π		π		π
Odp: x ∊ <		,−		> ∪ {−		,		}
	4		4		2		2

tryg:

	3
a nie −		π ?
	4

Godzio: Co Ci znowu nie pasuje ?

tryg:

	π		π
x=		lub x=π−		?
	4		4

Godzio: Proponuję wrócić do podstaw trygonometrii widać że masz ubytki

tryg: moze i ten jeden raz amsz racje.. ale nauczycielem nie badz.. troche dzieki

Godzio: No czasami mi się zdarza mieć więcej razy niż tylko raz