zadania z matmy mrovek: Mam takie zadanka z matmy, moze moglby mi ktos pomoc to zrobic bardzo prosze pozdrawiam 1. Ile liczb naturalnych pomiędzy 1 i 500 (włącznie) jest podzielnych dokładnie przez jedną z liczb 2, 11 i 13. 2. Ile liczb parzystych z przedziału [100, 9999] ma różne cyfry. 3.Pokazać, że wśród 18 liczb całkowitych istnieją co najmniej dwie, których różnica jest podzielna przez 17. 4.Rozwiązać równanie rekurencyjne an+1 = −8an −16an−1 , n >0, warunki początkowe a0 = 5, a1 =17

think: zad.1 liczb parzystych jest 250 z nich trzeba odrzucić parzyste wielokrotności 11 i 13 11,22, 33, 44,..., 484, 495 ← a₁ = 22; a_n = a₁ + (n − 1)r 484 = 22 + (n − 1)*22 n − 1 = 21 ⇒ n = 22 czyli 22 liczby są wielokrotnościami parzystymi, a wielokrotności nieparzystych jest 23. 13, 26, 39, 52, ..., 481, 494 ← a₁ = 26; a_n = a₁ + (n − 1)r 494 = 26 + (n − 1)*26 n − 1 = 18 ⇒ n = 19 czyli odrzucamy 19 wielokrotności parzystych, ale dodajemy 19 wielokrotności nieparzystych. Zostaje policzyć ile w tym przedziale jest liczb, które są wielokrotnością 11 z 13. 143, 429 i te też trzeba odjąć. Ostatecznie takich liczb jest 250 − 22 + 23 − 19 + 19 − 2 = 249.

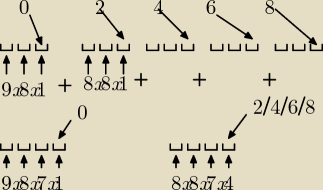
think: zad 2 dla 3−cyfrowych 9*8*1 + 4*8*8*1 = 72 + 256 = 328 dla 4−cyfrowych 9*8*7*1 + 8*8*7*4 = 504 + 1792 = 2296 więc wszystkich jest 328 + 2296 = 2624

mrovek: dzieki bardzo za 2 zadanka

łukasz: 2+2

bezendu: 2+2=log₂16

Kejt: 2+2=(4x)'

łukasz: ze zbioru liczb 1,2,3,4,5,6,7 losujemy 2 razy po jednej liczbie ze zwracaniem oblicz prawdopodobieństwo zdarzenia polegającego na wylosowaniu liczb których iloczyn jest podzielny przez 1 odpisz proszę szybko

Saizou : 2+2=sih (z japońskiego śmierć)

łukasz: umiesz to

łukasz: jest taki zadanie co roku na maturze tylko inne liczby obliczyc

bezendu:

bezendu: skoro co rok jest na maturze to masz schemat to tylko zamień liczby

Saizou : przez 1 dzieli się każda liczba naturalna