Styczne Melody: Mamy dwa okręgi (x+1)²+(y−3)²=4 oraz (x−5)²+(y−3)²=4. Należy znaleźć proste styczne do obu okręgów. Te poziome łatwo znaleźć, nie mam pojęcia jak znaleźć te "na ukos". Jedyne do czego zdołałem dojść, to to że obie przecinają środek odcinka pomiędzy środkami okręgów.

Basia: S₁ = (−1,3) r₁=2 S₂ = (5,3) r₂ = 2 S₁S₂ = 6 okręgi są położone zewnętrznie y = ax+b każdy z układów (x+1)²+(y−3)²=4 y = ax+b (x−5)²+(y−3)²=4 y=ax+b musi mieć jedno rozwiązanie teraz wykorzystaj to do czego doszłaś prosta przechodzi przez punkt P(2,3) 3 = 2a+b b = 3−2a y = ax+3−2a podstaw do układu równań Δ musi =0 (zdaje się, że jeden wystarczy rozwazyć)

Melody: Dziękuję bardzo

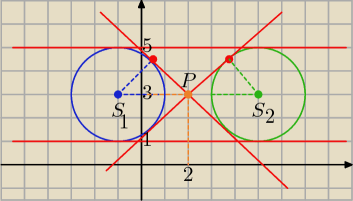
Eta: są 4 takie styczne: 1: y= 1 2: y= 5 3 i 4 : y= ax+b , P(2,3) to: 3= 2a+b => b= 3−2a y= ax =3 −2a ......... ( podobnie jak napisała Basia można dalej tak jak podaje Basia lub prościej jest wyznaczyć styczne z tego,że odległość S od stycznych = r= 2 styczna: ax−y +3 −2a=0 i S₁(−1,3)

	|−a−3 +3−2a|
d=		= 2
	√a2+1

|−3a|= 2√a²+1 /² 9a² = 4a² +4 => 5a²=4

	2√5		2√5
a=		lub a= −
	5		5

	4√5		4√5
to: b= 3−		lub b= 3+
	5		5

styczne 3 i 4 mają równania: y= .......... y=.........