:<
Cayman: Prosze Pomóżcie Oblicz pole prostokąta o obwodzie 70 cm, wiedząc, że długości jego boków
oraz przekatnej tworzą ciąg arytmetyczny.
6 lut 18:23
Kejt: Ułóż trzy układy.. korzystając z:
1) obwodu prostokąta
2) własności ciągu arytmetycznego
3) twierdzenia pitagorasa..
6 lut 18:25
Kejt: układ z trzech równań*
6 lut 18:26
Cayman: No właśnie wiem, ale nie jarze tego :< mogę robić tożsamości trygonometryczne alpo operacje na
ciągach a nie moge sobie poradzić z takim gównem pomóż :<
6 lut 18:30
Cayman: Pomóż ktoś.. :L<
6 lut 18:35
Kejt:
a − długość krótszego boku prostokąta
b − długość dłuższego boku prostokąta
c − długość przekątnej
1)2a+2b=70
a+b=35
2b=a+c
3) a
2+b
2=c
2
i mamy układ:
a+b=35
a
2+b
2=c
2
1) a+b=35
b=35−a
do drugiego:
2(35−a)=a+c
do trzeciego:
a
2+(35−a)
2=c
2
i mamy układ z dwiema niewiadomymi:
2(35−a)=a+c
a
2+(35−a)
2=c
2
z tym powinieneś sobie poradzić.. gdyby nie, pytaj.
6 lut 18:37
Cayman: c = 35?
6 lut 18:42
Cayman: Kurde no dalej nie wiem nic :< mógłbyś mi to albo zrobić abo przedstawić jak dla matoła ?
6 lut 18:44
6 lut 18:55
Kejt: mogłabyś.. czego nie rozumiesz?
6 lut 19:03
Cayman: nie wiem kompletnie nic nigdy tego nie mogłem zajarzyć a do 20 musze oddać zadanie :<
6 lut 19:10
Kejt: ech.. powiedz szczerze.. nie chce Ci się i chciałbyś żeby ja to zrobiła czy naprawdę nie
rozumiesz?
6 lut 19:11
Cayman: nie rozumiem ...
6 lut 19:16
Cayman: gdybym rozumiel to nawety bym Cie nie meczyl
6 lut 19:17
Kejt: dobra.. postaram się łopatologicznie to rozpisać i rozwiązać.. daj chwilkę..
6 lut 19:18
Cayman: Dzięki
6 lut 19:20
Cayman: i jak masz ?
6 lut 19:37
Kejt:
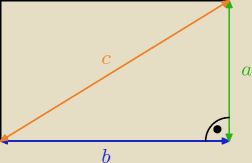
a<b<c
z racji, że są to długości odcinków, nie mogą być ujemne więc a,b,c>0
1)obwód prostokąta wynosi 70cm, wzór na obwód:
Ob=2a+2b
podstawiamy:
70=2a+2b /:2
i mamy pierwsze równanie, które możemy trochę "uporządkować":
70=2a+2b /:2
35=a+b
wyprowadzamy jedną z niewiadomych, powiedzmy 'b':
35=a+b /−a
35−a=b
b=35−a
i mamy pierwsze równanie do naszego układu
2) aby ułożyć drugie równanie korzystamy z własności ciągu arytmetycznego, własność tego ciągu:
dotyczy ona trzech kolejnych wyrazów: a
n−1; a
n; a
n+1
przy naszych oznaczeniach to kolejno: a; b; c
czyli:
a
n−1=a
a
n=b
a
n+1=c
podstawiamy do naszego wzoru:
i mamy kolejne, drugie równanie, które porządkujemy:
2b=a+c
3) mamy tu, jak widać na rysunku do czynienia z trójkątem prostokątnym, więc możemy skorzystać
z twierdzenia Pitagorasa:
a
2+b
2=c
2
które akurat pasuje do naszych oznaczeń, wiec nie trzeba nic podstawiać ani zmieniać.
mamy więc trzy równania.
z pierwszego mamy wyprowadzone b:
b=35−a
możemy więc podstawić to do dwóch pozostałych równań:
do 2):
2b=a+c
2(35−a)=a+c
do 3):
a
2+b
2=c
2
a
2+(35−a)
2=c
2
i mamy układ równań z dwiema niewiadomymi:
2(35−a)=a+c
a
2+(35−a)
2=c
2
wyprowadzam z pierwszego niewiadomą 'c':
2(35−a)=a+c
2(35−a)−a=c
c=2(35−a)−a
upraszczam:
c=2(35−a)−a
c=70−2a−a
c=70−3a
podstawiam to do drugiego równania:
a
2+(35−a)
2=c
2
a
2+(35−a)
2=(70−3a)
2
i liczę 'a':
a
2+(35−a)
2=(70−3a)
2
najpierw korzystam ze wzorów skróconego mnożenia:
a
2+1225−70a+a
2=4900−420a+9a
2 /−9a
2 /+420a /−4900
−7a
2+350a−3675=0 /:7
−a
2+50a−525=0
Δ=b
2−4ac=2500−2100=400
√Δ=20
| | −b−√Δ | | −50−20 | | −70 | |
a1= |
| = |
| = |
| =35 |
| | 2a | | −2 | | −2 | |
| | −b+√Δ | | −50+20 | | −30 | |
a2= |
| = |
| = |
| =15 |
| | 2a | | −2 | | −2 | |
podstawiamy dla a
1:
c
1=70−3a
c
1=70−3*35
c
1=70−105
c
1=−35
c
1<0
czyli nie spełnia założeń.
podstawiamy dla a
2:
c
2=70−3*15
c
2=70−45
c
2=25
podstawiam a
2 do pierwszego równania:
b=35−a
b=35−15
b=20
a=15
b=20
c=35
bardziej łopatologicznie już naprawdę nie umiem..ale jakby co to pytaj.. (mam nadzieję, że się
nigdzie nie walnęłam...)
6 lut 19:51
Kejt: no oczywiście walnęłam.. w ostatniej linijce c=25..
6 lut 19:53
6 lut 19:58
Kejt: jeśli zrozumiałeś.. to stawiasz mi za to piwo..
6 lut 19:58
