| 3−p | ||
x = | ||
| 2 |
| 3−p | 3−p | ||
≥0 i | <3 | ||
| 2 | 2 |
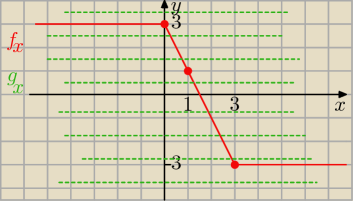 Można też odczytać korzystając z wykresów :
f(x) = |x −3| − | x | , g(x)= p
dla x <0 f(x) = −x +3 +x = 3
dla x€ <0,3) f(x) = −x +3 −x= −2x +3
dla x≥3 f(x) = x−3 −x = −3
{ 3 dla x <0
f(x)= { −2x +3 dla 0≤ x <3
{ − 3 dla x≥3
wykresy f(x) i g(x) przecinają się w jednym punkcie <=> p€(−3, 3)
Odp: dla p€(−3,3) −−−−−− jedno rozwiązanie
dla p = −3 lub p= 3 −−−−− niesk. wiele rozwiązań
dla p €( −∞, −3) U (3, ∞) −−− brak rozwiązań
Można też odczytać korzystając z wykresów :
f(x) = |x −3| − | x | , g(x)= p
dla x <0 f(x) = −x +3 +x = 3
dla x€ <0,3) f(x) = −x +3 −x= −2x +3
dla x≥3 f(x) = x−3 −x = −3
{ 3 dla x <0
f(x)= { −2x +3 dla 0≤ x <3
{ − 3 dla x≥3
wykresy f(x) i g(x) przecinają się w jednym punkcie <=> p€(−3, 3)
Odp: dla p€(−3,3) −−−−−− jedno rozwiązanie
dla p = −3 lub p= 3 −−−−− niesk. wiele rozwiązań
dla p €( −∞, −3) U (3, ∞) −−− brak rozwiązań