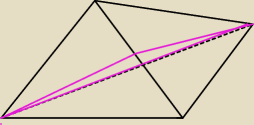
 Czworościan foremny o krawędzi długości a przecięto płaszczyzną przechodzącą przez krawędź
podstawy i nachyloną do płaszczyzny podstawy pod kątem 60 stopni . Obliczyć pole otrzymanego
przekroju.
Czworościan foremny o krawędzi długości a przecięto płaszczyzną przechodzącą przez krawędź
podstawy i nachyloną do płaszczyzny podstawy pod kątem 60 stopni . Obliczyć pole otrzymanego
przekroju.
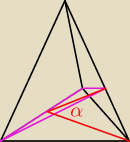
| Pprzekroju | ||
cosα= | ||
| Ppodstawy |

| a2√3 | ||
Nie mam takiej odpowiedzi.. a wychodzi mi | ||
| 8 |
| 1 | ||
c) | a2√2}(3−√6) | |
| 2 |
| 1 | ||
d) | a2√3(3−√2) | |
| 2 |
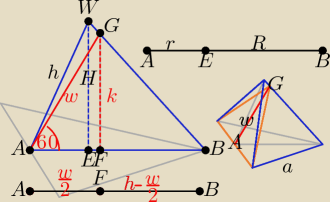 Czworościan foremny:
Czworościan foremny:
| 1 | 1 | 1 | 1 | |||||
H = | a√6, r = | a√3, R = | a√3, h = r + R = | a√3 | ||||
| 3 | 6 | 3 | 2 |
| 1 | 1 | |||
|AG| = w, |AF| = | w, |FG| = k = | w√3 | ||
| 2 | 2 |
| 1 | ||
Pole zadanego przekroju P = | aw | |
| 2 |
| H | k | ||||||||||||
Z podobieństwa trójkątów WEB i GFB: | = | ||||||||||||
| R |
|
|
| ||||||||||||||||||||||||||
= | |||||||||||||||||||||||||||
|
|
| w√3 | ||
√2 = | stąd wyznaczyć trzeba w | |
| a√3 − w |
| a√6 | ||
w= | ||
| √3+√2 |
| a√6(√3−√2) | ||
w= | ||
| 3−2 |
| 1 | ||
Pole powinno wynosić | a2√6(√3−√2) a to znaczy | |
| 2 |
| 1 | ||
P= | a2(√18−√12) | |
| 2 |
| 1 | ||
P= | a2(3√2−√6*√2) | |
| 2 |
| 1 | ||
P= | a2√2(3−√6) | |
| 2 |
