Nierówność Ania: rozwiąż nierówność x + x / (2x −1) ≤1

Niunia85:

	x
x+		−1≤0 /*2x−1
	2x−1

2x²−x+x−2x+x≤0 2x²+−x≤0 x(2x−1)≤0 x₁=0

	1
x2=
	2

	1
x∊<0,		>
	2

ICSP: Niunia a przypadek kiedy x jest ujemne

Kiki: Dziękuje

ICSP: Wygląda na to że będę musiał się sam przyjrzeć.

	x		2x2 − x + x − 2x + 1		2x2 − 2x + 1
x +		−1 ≤ 0 ⇔		≤ 0 ⇔		≤ 0 . Delta
	2x−1		2x−1		2x−1

w tym trójmianie kwadratowym nie ma pierwiastków wiec nie ma problemu. Teraz przemnażamy przez kwadrat mianownika:

	1
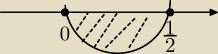
(2x2 − 2x + 1)(2x−1) ≤ 0 . Pierwiastki tego wielomianu to		. Tutaj rysujemy wykres i
	2

	1
podajemy odpowiedz że x ∊ (− ∞ ;		)
	2