Ostrosłup Iza: W ostrosłupie prawidłowym trójkątnym krawędz podstawy ma długość a=5 , a krawędz boczna jest nachylona do płaszczyzny podstawy pod kątem (alfa)=45(stopni). Oblicz pole powierzchni całkowitej i objetości tego ostrosłupa. Prosze o pomoc za kazdym razem wychodzi co innego ....

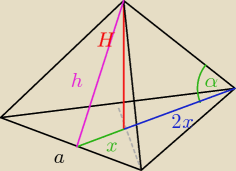Trivial: a = 5 α = 45^o

	a2√3
Pp =
	4

	a√3
hp =		= 3x
	2

	a√3
2x =
	3

	H		a√3
tgα =		→ H = 2x*tgα =		*tgα
	2x		3

	1		1		a2√3		a√3		a3
V =		Pp*H =		*		*		*tgα =		*tgα.
	3		3		4		3		12

x² + H² = h² x² + 4x²*tg²α = h² x²(1 + 4tg²α) = h² h = x√1+4tg²α.

	1		3		a√3		a2√3
Pb = 3*		*a*h =		*a*(		√1+4tg2α) = (		√1+4tg2α).
	2		2		6		4

	a2√3
Pc = Pp + Pb =		(1 + √1+4tg2α).
	4

Mam nadzieję, że dobrze.

Iza: dziekuje

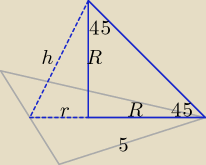Bogdan: Wykorzystajmy dane zadania od razu:

	5
R − długość promienia okręgu opisanego na trójkącie równobocznym, R =		√3
	3

	5
r − długość promienia okręgu wpisanego w trójkąt równoboczny, r =		√3
	6

	75		75		25*15		5
h2 = R2 + r2 =		+		=		⇒ h =		√15
	9		36		36		6

	1		1		5
Objętość V =		*		*25√3*		√3 = ...
	3		4		3

	1		1		5
Pole P =		*25√3 + 3*		*5*		√15 = ...
	4		2		6