całki i kłopot z ich obliczeniem
karola171991: całki i kłopot z ich obliczeniem
jak z ∫
10 √ 1+ 4x2 dx otrzymać
| 1 | | 1 | |
| √ 5 + |
| ln (2 + √ 5 ) |
| 2 | | 4 | |
| | 1 | | −x | | 1 | |
oraz ∫ |
| 0 √ 1 + ( |
| dx = ∫ |
| |
| | 2 | | √ 1−x2 )2 | | 2 | |
| | 1 | |
w tym drugim za dobrze tego nie widać górna granica całkowania to |
| a dolna to 0 |
| | 2 | |
oraz nie chce wyjść znak pierwiastku: 1 + ułamek: licznik x, mianownik: pierwiastek 1 − x
2,
cały ten wielki ułamek podniesiony jest do kwadratu
5 lut 19:30
karola171991:
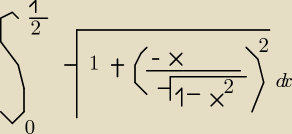
tak to miało wyglądać, trochę koślawo wyszło
5 lut 19:39
Trivial:
Druga:
| | −x | | x2 | | 1−x2 + x2 | | 1 | |
f(x) = 1 + ( |
| )2 = 1 + |
| = |
| = |
| . |
| | √1−x2 | | 1−x2 | | 1−x2 | | 1−x2 | |
| | 1 | | 1 | | π | |
∫01/2 √f(x)dx = ∫01/2 |
| dx = arcsin |
| − arcsin0 = |
| . |
| | √1−x2 | | 2 | | 6 | |
5 lut 19:47
karola171991: mam jeszcze jedno pytanie do przejścia którego nie rozumiem
dlaczego z
| | 1 | | 1 | |
∫{ |
| 0 √ |
| robi się |
| | 2 | | 1− x2 | |
5 lut 19:53
Trivial: √ 1 = 1.
5 lut 19:54
Trivial:
Pierwsza całka:
Jest wzór na takie całki, ale go nie pamiętam, więc zrobię ze współczynników nieoznaczonych.

| | 1+4x2 | | dx | |
∫√1+4x2dx = ∫ |
| dx = (Ax + B)√1+4x2 + k∫ |
| / ' |
| | √1+4x2 | | √1+4x2 | |
| 1+4x2 | | 8x | | k | |
| dx = A√1+4x2+(Ax+B) |
| + |
| / *√1+4x2 |
| √1+4x2 | | 2√1+4x2 | | √1+4x2 | |
1 + 4x
2 = A(1 + 4x
2) + (Ax + B)*4x + k.
x
2: 4A + 4A = 4
x
1: 4B = 0
x
0: A + k = 1
| | 1 | | 1 | |
A = |
| , B = 0, k = |
| . |
| | 2 | | 2 | |
| | 1 | | 1 | |
∫√1+4x2dx = |
| x√1+4x2 + |
| ln|x + √1+4x2| + c. |
| | 2 | | 2 | |
Teraz tylko zostało podstawienie i policzenie.

5 lut 19:57
karola171991: uchu....no cóż te współczynniki nie są na miarę moich możliwości, ale dzięki za odp
5 lut 20:00
Trivial:
Współczynniki nieoznaczone nie są trudne, ale zajmują dużo czasu... (i do tego strasznie
wyglądają

)
5 lut 20:01
magda: całka 2/x pierwiastek z x2−2 dx
8 wrz 10:34
Basia:
tak to ma być ?
czy inaczej ?
napisz porządnie jeżeli chcesz szybko uzyskać jakąś pomoc
8 wrz 10:38
magda: tak chyba tak moj chlopak ma poprawke i tak mi napisal sms
8 wrz 10:44
Basia: bardzo mi przykro, ale w oszustwach nie zamierzam uczestniczyć
8 wrz 10:45
Tomasz: a mnie interesuje to rozwiazanie moze napiszesz przyda mi sie a jest to ciekawa całka
8 wrz 10:46
Tomasz: całki u mnie leza...
8 wrz 10:46
Tomasz: Basia to bys rozwiazala, bylbym wdzieczny

8 wrz 10:47
magda: ok dzieki pa
8 wrz 10:48
Basia: niestety; teraz już nie mogę
pozostałych też proszę o powściągliwość
to jest nielegalne; może być ścigane z urzędu; a chyba nie chcemy, żeby Jakub miał kłopoty
8 wrz 10:48
Piotr:
chłopak
magdy...

8 wrz 10:48
Basia: i ciekawe kto jeszcze, bo żadnego z tych nicków nie ma.....................
8 wrz 10:50
tomasz: to na poczte wyslij rozwiaznie
8 wrz 10:50
M: całka 3x2+ 2x− x3 / x4 dx=
całka 3x2/ x4 + 2x/x4− x3/x4 dx= całka 3/x2 +2/x3− 1/x dx= 3 całka x−2 dx + 2 Całka
x−3 dx − całka 1/x dx= 3 x−1/−1 +2 x−2/−2 − ln (x) +c= −3/x+ −1/x2 − ln (x) +c
nie wiem czy ktos zrozumie bo ja nie umiem wstawiac tych znakow ale czy to jest dobrze
rozwiazane bo mi sie wydaje ze raczej tak aczykolwiek moze gdzies sie walnelam...?
8 wrz 11:29
M: wogole jak tu wstawic ulamki potege itp?
8 wrz 11:30
8 wrz 11:35
M: dzieki jestem slepa w takim razie bo to jest obok okienka do wpisywania
8 wrz 11:38
Basia: proszę zwracać uwagę na mój wpis z 10:48
8 wrz 11:38
M: rozumiem rozumiem ja rozwiazalm sama i chyba dobrze zrezszta okaze sie niebawem

8 wrz 11:40
M: moze przydaly mi sie nauki mojej siostry do czegos chociaz nie wiem bo ja troche tepa z matmy.
8 wrz 11:44
11 wrz 10:57
Ola: ∫x4lnxdx
25 maj 23:59
Nienor: Przez części.
| | 1 | | 1 | | 1 | | 1 | | 1 | | 1 | |
I= |
| x5lnx− |
| ∫x5* |
| dx= |
| x5lnx− |
| ∫x4dx= |
| x5 |
| | 5 | | 5 | | x | | 5 | | 5 | | 5 | |
| | 1 | | 1 | | 1 | | 1 | |
lnx− |
| * |
| x5+C= |
| x5(lnx− |
| )+C
|
| | 5 | | 5 | | 5 | | 5 | |
Sprawdzam czy się zgadza:
| | 1 | | 1 | | 1 | | 1 | | 1 | |
x4(lnx− |
| )+ |
| x5* |
| =x4lnx− |
| x4+ |
| x4=x4lnx
|
| | 5 | | 5 | | x | | 5 | | 5 | |
Zgadza się.
26 maj 00:07
Nienor: | | dx | | dx | |
Całki ∫ |
| , ∫ |
| chyba najprościej policzyć z p I podstawienia |
| | x√x2−2 | | x√x2+5 | |
Eulera.
Nie chce mi się liczyć obu. Pierwsza wygląda tak:
√x2−2=t+x ⇒ t=
√x2−2−x
x
2−2=t
2+2tx+x
2
−2=t
2+2tx
| | t2+2 | | 2t2−t2−2 | | t2−2 | |
t+x=t− |
| = |
| = |
| =√x2−2
|
| | 2t | | 2t | | 2t | |
| | −2t*2t+2(t2+2) | | −4t2+2t2+4 | | −t2+2 | |
dx= |
| dt= |
| dt= |
| dt
|
| | 4t2 | | 4t2 | | 2t2 | |
Podstawiając do całki:
| | 1 | | 1 | | −2t | | 2t | | −(t2−2) | | 2 | |
I=∫ |
| * |
| dx=∫ |
| * |
| * |
| dt=∫ |
| dt=
|
| | x | | √x2−2 | | t2+2 | | t2−2 | | 2t2 | | t2+2 | |
dt=
√2dz
| | √2 | | 1 | | t | |
I=∫ |
| dz=√2∫ |
| dz=√2arctgz+C=√2arctg |
| +C=
|
| | z2+1 | | z2+1 | | √2 | |
26 maj 00:21
karolina: | | 1 | |
proszę o rozwiązanie całki |
| albo chociaż o jakąś podpowiedź jak to zrobić  |
| | √1+y3 | |
25 mar 22:30
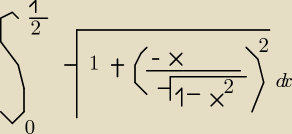 tak to miało wyglądać, trochę koślawo wyszło
tak to miało wyglądać, trochę koślawo wyszło


 )
)



