moduł
ula: proszę o pomoc

jak rozwiązać taką nierówność?
zadanie z modułem
/2+x/−3/x/<1+x
4 lut 22:45
Basia:
rozważ trzy przypadki:
1. x<−2
2. −2≤x<0
3. x≥0
4 lut 22:54
ula: dlaczego tak?
4 lut 22:58
Mila:
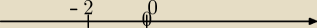
|2+x|−3|x|<1+x
wyznaczamy miejsca zerowe
2+x=0 x=0
x=−2
1) x∊(−
∞,−2) −2−x+3x<1+x
2) x∊<−2,0) 2+x+3x<1+x
3)x∊<0,
∞) 2+x−3x<1+x
∞
4 lut 22:59
Mila: wiesz dlaczego tak wygladaja nierówności ?
4 lut 23:05
ula: dlaczego są takie przedziały?
4 lut 23:06
Mila: Masz |2+x| kiedy będzie =0 ? |x| kiedy będzie =0 ?
4 lut 23:08
ula: to przedział będzie od (−2, ∞) i od (0,∞)
4 lut 23:10
Mila: spójrz na mój rysunek
4 lut 23:13
ula: ok już wiem

dziękuje ci bardzo
4 lut 23:14
Mila: umiesz dalej ?
4 lut 23:18
ula: tak juz wiem jak
4 lut 23:23
Mila: pamiętaj,ze po wyliczeniu x musisz sprawdzić czy mieści sie w przedziale
4 lut 23:25
ula: x=1/3 i x=−1/3
4 lut 23:27
ula: x<−1/3 i x>1/3 o tak

4 lut 23:29
Mila: 1) −2−x+3x<1+x x∊(−∞−2)
−2 +2x<1+x
x<3 i x∊(−∞ ,−2) odp x∊(−∞−2)
lub i teraz nastepne liczysz
4 lut 23:36
Mila: 2) 2+x+3x<1+x x∊<−2,0)
4x−x<1−2
3x<−1
x<−1/3 i x∊<−2,0) odp x∊<−2,−1/3)
lub i następny
4 lut 23:39
Mila:
2+x−3x<1+x x∊<0,∞)
2−1−2x<x
1<3x
x>1/3 i x∊<0,∞) x∊(1/3,∞)
Odp x∊(−∞,−2) v <−2,−1/3) v (1/3,∞)
4 lut 23:47
Mila: czyli x∊(−∞,1/3) v(1/3,∞)
4 lut 23:50
ula: własnie taki wyszedł mi wynik
5 lut 00:05
 jak rozwiązać taką nierówność?
zadanie z modułem
/2+x/−3/x/<1+x
jak rozwiązać taką nierówność?
zadanie z modułem
/2+x/−3/x/<1+x
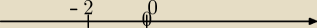 |2+x|−3|x|<1+x
wyznaczamy miejsca zerowe
2+x=0 x=0
x=−2
1) x∊(−∞,−2) −2−x+3x<1+x
2) x∊<−2,0) 2+x+3x<1+x
3)x∊<0,∞) 2+x−3x<1+x
∞
|2+x|−3|x|<1+x
wyznaczamy miejsca zerowe
2+x=0 x=0
x=−2
1) x∊(−∞,−2) −2−x+3x<1+x
2) x∊<−2,0) 2+x+3x<1+x
3)x∊<0,∞) 2+x−3x<1+x
∞
 dziękuje ci bardzo
dziękuje ci bardzo
