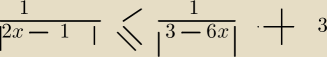Wartość bezwzględna z ułamkami (w ułamku) w nierównościach
Problemowa02: Witam! Czy ktoś mógłby napisać mi jak po kolei oblicza się wartość bezwzględną w takich
przykładach? Byłabym bardzo wdzięczna

4 lut 20:15
Basia:
ad.1
2 ≤ 3|x| /:3
|x|≥
23
x≥
23 lub x≤ −
23
drugie tak samo
ad.3
x≠0
tu już musisz rozważać przypadki
1.
x+2≥0 ⇔ x≥ −2 ⇔ x∊<−2,0)∪(0,+
∞)
|x+2|=x+2
i rozwiązujesz nierówność
y=x
2+2x−3
Δ=4+12=16
x(x+3)(x−1)>0 ⇔ x∊(−3,0)∪(1,+
∞)
stąd x∊[(−3,0)∪(1,+
∞)]∩[<−2,0)∪(0,+
∞)] = <−2,0)∪(1,+
∞)
2.
x+2<0 ⇔ x< −2 ⇔ x∊(−
∞,−2)
|x+2|=−(x+2) = −x−2
i rozwiązujesz nierówność
U{−x
2−2x−3}{x)>0 /*(−1)
y=x
2+2x+3
Δ=4−12<0
x
2+2x+3> 0 (stale)
stąd
x<0 ⇔ x∊(−
∞,0)
stąd x∊(−
∞,0)∩(−
∞,2) = (−
∞,2)
ostatecznie:
x∊[<−2,0)∪(1,+
∞)]∪(−
∞,−2) = (−
∞,0)∪(1,+
∞)
pozostałe tak samo
4 lut 20:34
Problemowa02: Rozumiem ale w przykładzie 2 odpowiedź wyszła mi x < 10 lub x > − 8 , a więc odpowiedzią będzie
suma tych przedziałów czyli x należy do (−8 ; 10)? a co do przykładu 5 i 6: w przykładzie 5 w
| | 3 | |
jednym przypadku wyszła mi nierówność sprzeczna a w drugim x ≥ |
| . a w przykładzie 6 |
| | 4 | |
wyszło mi x <4,5 lub x < 0,25, czyli x należy do (−∞ ; 4,5). Czy te odpowiedzi są poprawne?
4 lut 21:01
Basia:
ad.2
na pewno lub ? bo suma to zbiór ℛ
tam jest iloczyn i i wtedy x∊(−8,10)
ad.5 i 6
muszę przeliczyć
4 lut 21:07
Basia:
(5) jest dobrze
(6) nie; powinno być x∊(14; 53)∪(53, 92)
policz jeszcze raz
4 lut 21:28
roman: eeee sory Basia a czy jak w pierwszym przykładzie ( ad.1) dzielisz przez 3 , a ty 3 to
przecierz nie jest liczba ujemna wiec dlaczego zmieniałas znak >?
mozesz mi to wytłumaczyc .... czy ja jestem w błedzie >?
4 lut 21:58
Basia:
nie zmieniłam znaku tylko napisałam nierówność "z prawa na lewo"
23≤|x|
|x|≥23
4 lut 22:15
roman: ale ja jestem spostrzegawczy ..... no tak

dzieki Hej
4 lut 22:16
Problemowa02: Mogłabyś jeszcze rozpisać przykład 6? czemu są 3 przypadki a nie 2?
4 lut 22:21
Problemowa02: a w przykładzie 2 fakt będzie znak i ... po prostu źle spojrzałam
4 lut 22:23
Basia:
UWAGA !
Mogę sobie pozwolić na mnożenie, bo w tych przedziałach znam znak mianownika
m.zerowe: −4 i
53
x∊(−
∞,−4) ⇒
|x+4| = −(x+4) i |3x−5| = −(3x−5) ale
3x−5<0
stąd
x−4<3x−5
−2x<−1
x>
12
sprzeczność
x∊<−4,
53)
|x+4| = x+4
|3x−5| = −(3x−5) ale
3x−5<0
| x+4 | |
| <1 /*[−(3x−5)] to jest dodatnie |
| −(3x−5) | |
x+4<−(3x−5)
x+4<−3x+5
4x<1
x<
12
x∊<14,53)
x∊(
53,+
∞)
|x+4|=x+4
|3x−5| = 3x−5
| x+4 | |
| >1 /*(3x−5) to teraz jest dodatnie |
| 3x−5 | |
x+4>3x−5
−2x>−9
x<
92
x∊(53, 92
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
można inaczej
| x+4 | |
| ≥0 ⇔ x∊(−∞,−4>∪(53,+∞) |
| 3x−5 | |
i mam
ale teraz
nie wolno mi mnożyć, bo nie znam znaku mianownika
czyli
x∊(
53,
92)
−−−−−−−−−−−
i mam
czyli
x∊(
14;
53)
4 lut 22:53
Problemowa02: Dzięki. Teraz rozumiem

5 lut 12:09
Roxy: 1/4−x≤2
15 lis 12:40
Roxy:
1
_____
4−x. ≤2
15 lis 12:42
moneta:
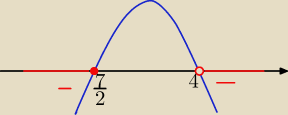
(4−x)(2x−7)≤0
x∊......................
15 lis 12:59
nemo:
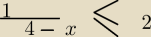
≤
15 lis 15:31
nemo:
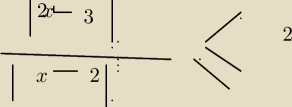
15 lis 15:39
nemo:
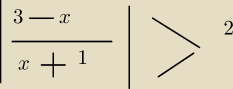
15 lis 15:42
nemo:

x
15 lis 15:47
nemo:
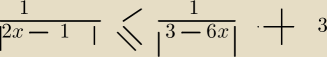
15 lis 15:52
Jerzy:
Masz jakiś problem z głową ?
15 lis 15:53
nemo: o co Ci chodzi? nie wiem jak to rozwiązać mozesz pomóc zamiast głupio komentować
15 lis 15:58

 dzieki Hej
dzieki Hej


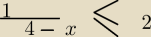 ≤
≤
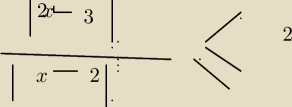
 x
x