Adnrzej kiełbasa Funkcja liniowa Jeruzalem: 1.60 Naszkicuj wykres funkcji f(x) = ||x−2|−2|−2, a następnie określ w zależności od parametru k, liczbę rozwiązań równania f(x) = k Z góry dzieki

Godzio: Pomogę

Jeruzalem: dzięki godzio

Jeruzalem: Najbardziej mam właśnie mam problem z rysowaniem wykresów funkcji z wartością bezwzględną nie wiem kiedy obija się symetrycznie względem OY kiedy OX

Godzio: 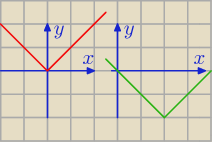_{przesunięcie o wektor [2,−2]} f(x) = |x| ⇒ |x − 2| − 2

Godzio: 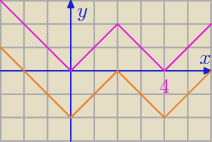_{symetria częściowa względem OX przesunięcie o wektor [0,−2]} ⇒ ||x − 2| − 2| ⇒ ||x − 2| − 2| − 2 dla k ∊ (−∞,−2) ⇒ brak rozwiązań dla k ∊ (0,∞) ∪ {−2} ⇒ 2 rozwiązania dla k = 0 ⇒ 3 rozwiązania dla k ∊ (−2,0) ⇒ 4 rozwiązania

Godzio:

	|x| + 1
na samego x np.		⇒ względem OY
	|x| − 1

	x + 1
na całą funkcję np. |		| ⇒ względem OX
	x − 1

Jeruzalem: dzięki bardzo

Violline: cześć, czy ktoś jest w stanie wytłumaczyć mi co się wgl robi aby obliczyć możliwości podstawienia tego parametru? nie rozumiem tego kompletnie, a przepisanie rozwiązań mnie nie satysfakcjonuje. z góry dziękuję