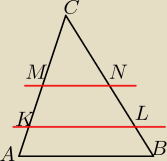
Planimetria ICSP: W trójkącie ABC poprowadzono dwie proste równoległe do boku AB. Podzieliły one trójkąt na figury o równych polach. Oblicz długości odcinków na jakie te proste podzieliły bok AC, jeśli ma długość 3√3. Problem mam w tym zadaniu że wprowadziłem 9 zmiennych i ułożyłem układ równań z 7 niewiadomymi(za mało równań). Jednak musi być jakiś prosty sposób. Mozę jakaś podpowiedz? Wiem że muszę skorzystać z twierdzenia Talesa i możliwe że również z podobieństwa trójkątów.

Eta: Witam jeżeli figury:

	Pf1
f1 ~ f2 w skali k =>		= k2 , k >0
	Pf2

	√6
ΔMNC ~ ΔABC w skali k12= 23 , k>0 to k1=
	3

	√3
ΔKLC ~ ΔABC w skali k22= 13 , to k2=
	3

i mamy:

	|CK|		√6
		=
	|AC|		3

	|CM|		√3
		=
	|AC|		3

Myślę,że już dalej sobie poradzisz odp: od góry od punktu C : 3 , 3(√3−√2) , 3(√2−1)

Eta: i znów ten chochlik mi namieszał ( wrrrrr) oczywiście ma być: ΔKLC ~ΔABC w skali k₁²= ²₃ ΔMNC ~ ΔABC w kali k₂²= ¹₃ Sorry , za ten poprzedni zapis

Eta: @ ICSP ........ pasuje?

ICSP: Dzięki bardzo Nie wpadł bym na to sam.

ICSP: Wiem ze to nic w odpowiedziach nie zmienia, ael czy boki nie powinny być inaczej ułożone od wierzchołka C? To znaczy: 3 , 3(√2−1) , 3(√3 − √2)