trójkąt
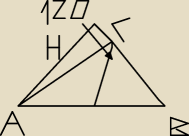
obrus: Ruszcie to zadanko...W trójkącie ABC dane są: <ACB=120, AC=6, BC=3. Dwusieczna <ACB przecina
bok AB w punkcie D.
Oblicz długość CD. Jaki jest zwiazek między dł. promieni: okręgu opisanego na trójkacie ADC i
okręgu opisanego na DBC?
2 lut 22:16
nate: Czy mozna zatosować wzór na pole trójkata 1/2*a*b*sin alfa przy alfa=120?
2 lut 22:23
obrus: właśnie tak próbowałem ale dziwne liczby wychodzą...
2 lut 22:24
Bogdan:
Można
2 lut 22:40
obrus: ale jakies chore pierwiastki wychodzą a ja mam w odp ze ten odcinek=2
2 lut 22:42
Bogdan:
Pokaż swoje obliczenia
2 lut 22:43
obrus: P ABC= 1/2*6*3*√3/2
P=1/2*3*H
H=3√3 −−TO JEST WYS POPROWADZONA Z C POZA TRÓJKATEM, POŻNIEJ WYCHODZI DŁ.ODCINKA OD WYSOKOŚCI
DO C=3, WIĘC CAŁY BOK MA 6 I Z PITAGORASA BOK AB WYCHODZI √63
2 lut 22:52
Godzio: banał
na pole trojkąta mozna to zrobic spokojnie.
2 lut 22:54
Godzio:
Zmień nick na inny
2 lut 22:55
obrus:
2 lut 22:58
obrus: MAŁO CHWYTLIWY TAKI NICK?
2 lut 22:58
Godzio:
To nie było do Ciebie
, "banał ..." −− to nie napisałem ja tylko mój sobowtór
2 lut 23:00
obrus: ALE TO ROBIĆ TAK JAK ZACZĄŁEM CZY MASZ COŚ PROŚCIEJ?
2 lut 23:01
Bogdan:
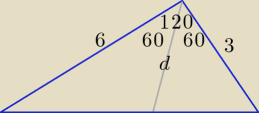
sin120
o = sin60
o
| 1 | | 1 | | 1 | | 2 | |
| *6*3*sin120o = |
| *6*d*sin600 + |
| *d*3*sin60o / * |
| |
| 2 | | 2 | | 2 | | 3sin60o | |
6 = 3d ⇒ d = 2
2 lut 23:10
Bogdan:
i co obrus − wszystko jasne?
2 lut 23:24