Zadnia Godzio: Eta Bogdan ! Miałbym do was prośbę, dało by radę żebyście napisali mi parę takich typowych zadanek konkursowych, ale nie aż znowu jakiś mega trudnych

Eta: Pomyślę....... (bo narazie to jestem trochę chora, grypsko mnie zmogło Bogdan jest mistrzem ! więc zapewne zaserwuje..... odpowiednie dla Ciebie zadanka

Godzio: W takim razie życzę Ci szybkiego powrotu do zdrowia

Konrad: jaki poziom?

Godzio: Liceum

b.: Tu jest mnóstwo: http://www.mimuw.edu.pl/OM/index2.php?poziom=9&main=zadania.php

Godzio: To już widziałem tylko tam większość to są raczej rzeźnicze a ja potrzebowałbym poćwiczyć do takiego wewnątrz szkolnego

Konrad: maturki sobie porób. ja ci moge wyslac tylko takie jak kolega wyzej wkleil i podobne (też do liceum chodze )

b.: niektóre zadania z I serii, szczególnie pierwsze 4 (to tak na zachętę) są trochę mniej rzeźnicze −− ale ogólnie trzeba dużo rozwiązywać po prostu −− na początku trochę pomyśleć samemu (powiedzmy 0.5 h), i jak nie ma się pomysłu −− zobaczyć rozwiązanie. Z czasem coraz częściej będziesz miał pomysły i coraz rzadziej będziesz musiał zaglądać do rozwiązań... Żeby takie ćwiczenia przyniosły efekt, myślę że muszą trwać co najmniej kilka miesięcy (systematycznie!) −− jeśli ten konkurs masz np. za tydzień, to jest bardzo mała szansa, że trafisz na coś podobnego do tego, co już ćwiczyłeś. Np. jeśli przygotowujesz się do OM w następnym roku szkolnym, dobrze zacząć rozwiązywanie zadań już teraz.

b.: P.S. Nie wiem co to za konkurs będzie, ale robienie 'maturek', jak sugeruje kolega wyżej, niewiele Ci moim zdaniem da... (no chyba że to jakieś maturki z lat 70 )

Godzio: Konkurs jeszcze nie wiem kiedy dokładnie, ale się zbliża Spróbuję porobić trochę z tej I serii mam nadzieję że coś się uda

Bogdan: Zadanka treningowe na początek. 1) Rozwiązać układ równań: x^y = y^x i x² = y³ 2) Wykazać, że dla dowolnego kąta ostrego α zachodzi: a) sinα + cosα ≤ √2 b) tgα + ctgα ≥ 2 3) Czy dla pewnego kąta ostrego α liczby sinα i cosα mogą być jednocześnie wymierne. 4) Czy z odcinków o długościach: 2²⁰¹⁰, 2²⁰¹¹, 2²⁰¹² można zbudować trójkąt? 5) Wyznaczyć pole trapezu o kątach ostrych 30^o i 60^o wiedząc, że różnica kwadratów długości jego przekątnych jest równa 20.

Godzio: Dzięki To na początek: 2)

	√2		√2		π
a) sinα + cosα = √2(		sinα +		cosα) = √2sin(α +		)
	2		2		4

	π
sin(α +		) ≤ 1 / * √2
	4

	π
√2sin(α +		) ≤ √2
	4

	sin2α + cos2α		1		1
b) tgα + ctgα =		=		= 2 *
	sinαcosα		sinαcosα		sin2α

	1		1
0 ≤ sin2α ≤ 1 ⇒		≥ 1 ⇒ 2 *		≥ 2
	sin2α		sin2α

4) Aby można było utworzyć trójkąt musi być spełniona nierówność: 2²⁰¹⁰ + 2²⁰¹¹ > 2²⁰¹² 3 * 2²⁰¹⁰ > 2²⁰¹² 3 > 4 ⇒ sprzeczność więc nie można utworzyć trójkąta

bart: skad sie wzielo 3*2²⁰¹⁰ ?

Grześ: wyłączył 2²⁰¹⁰ i wykonał w pamięci sobie (hoho ) 1+2=3

Konrad: 2²⁰¹⁰+2{2011)=2^{2010)*(1+2)

Konrad: 2²⁰¹⁰+2²⁰¹¹=2²⁰¹⁰*(1+2)

bart: no dobra, spokojnie Grypa mnie bierze i nie wszystko kojarze

Godzio: 1) Żeby zadanie miało rozwiązanie to y,x > 0 x^y = y^x

	2
x2 = y3 /3√ ⇒ y = x2/3 ⇒ xx2/3 = x2/3x ⇒ x2/3 =		x ⇒
	3

	2		27		3
x−1/3 =		⇒ x =		⇒ y =
	3		8		2

Nie mam pojęcia jak dojść do oczywistego rozwiązania jakim jest x = 1, y = 1 hmmm

Grześ: wg mnie przy opuszczaniu potęgi i porównywaniu wykładników możnaby jakiś komentarz dać, że dla x=1 jest spełniona równość. Potem rozpatrzyć x≠1 i wtedy porównać wykładniki. Chyba to by było okeeej

Godzio: Ano w sumie, bo f. wykładnicza nie jest określona dla 1 bo to po prostu funkcja stała by była

Grześ: nadal Godzio próbuje to ostatnie rozgryżć... też coś ćwiczę przed olimpiadą Coś próbuje układem etc.

Godzio:

	x
ctg30o =		⇒ x = √3h
	h

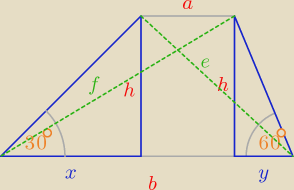
	y		√3
ctg60o =		⇒ y =		h
	h		3

e² − f² = 20 f² + h² = (x + a)² e² + h² = (y + a)² − −−−−−−−−−−−−−−−−−−−

	2		4
f2 − e2 = (x + a − y − a)(x + a + y + a) ⇒ 20 =		√3h(		√3h + 2a) /:4
	3		3

	1		15 − 2h2
5 =		h(2h + √3a) ⇒		= a
	3		√3h

	15 − 2h2		4		15 − 2h2
a + b =		+		√3h +		=
	√3h		3		√3h

	30√3 − 4√3h2		4√3h2		30√3		10√3
=		+		=		=
	3h		3h		3h		h

	a + b		5√3
P =		* h =		* h = 5√3
	2		h

Godzio:

Grześ: hoho.... właśnie zobaczę jak ty to zrobiłeś

Godzio: Dobra to teraz 3 trzeba ruszyć

Grześ: 3 akurat wg mnie proste. Chyba wystarczy podać jeden przykład dla takiej sytuacji Wtedy będzie pełny dowód

Godzio: 3) Teraz czekam na potwierdzenie, moim zdaniem wystarczyło by napisać że jest nieskończenie wiele takich kątów dla których sinα i cosα są wymierne bo wystarczy wziąć dowolny trójkąt prostokątny o całkowitych długościach boków i wyznaczyć sinus i cosinus dowolnego kąta ostrego

Godzio: Coś mi się ubzdurało na początku nie pytaj

Grześ: hehe... rozumiem A może Godzio zajrzysz do mojego zadania Ciągle głowę się jakiego można użyć tutaj przekształcenia

Bogdan: Zadania 1, 2, 3 i 4 zrobione. Jeszcze zadanie 5. Zadanie 5 proszę rozwiązać prostszą metodą. Uzasadnienie dla zadania trzeciego jest wystarczające. Ciąg dalszy treningu. 6) a) Czy liczba 11111111 jest pierwsza? b) Czy liczba 7777777 jest kwadratem liczby naturalnej? 7) Znajdź wszystkie liczby naturalne n takie, że liczby 5ⁿ − 2 i 5ⁿ + 2 są pierwsze.

	α + β		tgα + tgβ
8) Wykazać, że jeżeli 0 < α < β < π2, to: tg		<		.
	2		2

9) Wykazać, że jeżeli a, b, c > 1, to: log_a c + log_b c ≥ 4log_ab c. 10) Czy z każdego rosnącego ciągu liczb naturalnych można wybrać ciąg geometryczny? Pomijam w zadaniach polecenie, że wszystkie odpowiedzi należy uzasadnić, bo to się rozumie samo przez się.

Godzio: 6. a) Nie ponieważ liczba dzieli się przez 11, wynika to z jej cechy podzielności: 1 − 1 + 1 − 1 + 1 − 1 + 1 − 1 = 0, 0 dzieli się przez 11 b) 7777777 = 7 * 1111111 1111111 = 7k (musi być tej postaci aby był to kwadrat liczby naturalnej) ⇒ z cechy podzielności przez 7: 1111 − 111 = 1000 ≠ 7p więc liczba nie jest kwadratem liczby naturalnej

AC: Rozwiązaniem, równania x^y = y^x jest zawsze para (x; x) gdzie x > 0 np. x=3 i y=3 3³ = 3³

Grześ: taaa, ale tam jest układ równań. Poza tym to nie jest do konca jednoznaczne.. spójrz na jedną parę rozwiązań, któa nie należy do Twojej wskazanej, czyli:

	27
x=
	8

	3
y=
	2

Karol: ja wiem ze to nie ten temat ale chciałbym tu obecnym podziękować za pomoc − zdałem majce w zerówce

b.: Inne rozwiązanie 6b: kwadrat liczby naturalnej nie może się kończyć siódemką (albo nieco ogólniej, nie może dawać przy dzieleniu przez 5 reszty 2). Na tą samą modłę: dla jakich n, liczba 99..9 (n cyfr, każda to dziewiątka) jest kwadratem l.całkowitej?

Kejt: wybacz, że Ci się do tematu wtrącam.. ale masz błąd w jednym zadaniu (tym co mi dałeś)

Godzio: Wiem , pisałem że w kilku są błędy ale nie chciało mi się już poprawiać bo było już po skanowaniu także w 2−4 zadaniach jest błąd

Kejt: 2−4? ja znalazłam w 15..

Godzio: w 15 zadaniach były błędy ?

Kejt: mi chodziło o numer zadania chyba się nie zrozumieliśmy

Godzio: Ale mnie przestraszyłaś , Teraz patrzę to tak w 15 jest błąd w 11 także co do innych nie wiem bo nie pamiętam

Kejt: wybacz. nie kontaktuję już chyba. na 11 nawet nie patrzyłam.. no nic. dobranoc

Godzio: Ano dobranoc ja się jeszcze będę męczyć z tym 5 muszę znaleźć jakiś prosty sposób

Kejt: które 5?

Godzio: To co jest tam wyżej 20:51, zrobiłem je niby ale trzeba prostszym sposobem

Bogdan: i to znacznie Godzio prostszym sposobem

Godzio: Muszę chwilkę odpocząć bo zaraz mi mózg wyparuje za 20 min ruszam dalej

Bogdan: Będąc w klasie przedmaturalnej też walczyłem z tym zadaniem. Jego autorem jest jeden z moich nauczycieli. Ocena za to zadanie zależała od sposobu jego rozwiązania. Im prostsze rozwiązanie, tym wyższa ocena. Tym razem nie udzielę żadnych wskazówek i pozostawiam Tobie oraz wszystkim chętnym przyjemność w szukaniu tego najprostszego rozwiązania

Konrad: korzystajac z kątów, oznaczam prawą krawędź jako 2b. wówczas y=b x=3b f²−e²=20 (3b+a)²+3b² = f² (b+a)²+3b²=e² − wstawiamy wyżej 12b²+6bc+c² − (b²+2bc+c²+3b²)=20 8b²+4bc=20 2b²+c=5

	5−2b2
c=		− wstawiamy do pola
	b

	5−2b2   5−2b2   [ + +4b]*b√3   b   b		10−4b2   4b2   [ + ]*b√3   b   b
P=		=
	2		2

	10   *b√3 b		10√3
P=		=		=5√3
	2		2

ja bym tak zrobił

Konrad: cholercia, oczywiscie zamiast każdego "c" powinno być "a"

Bogdan: Konrad − jest prostsze rozwiązanie

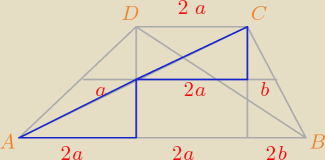
Godzio: To chyba prostszy znalazłem

	h		2√3
tg30 =		=> h =		a
	2a		3

	h		1
tg60 =		=> h = 2√3b ⇒ b =		a
	2b		3

e² = h² + (4a)² f² = h² + (2a + 2b)² − −−−−−−−−−−−−−−−−−−−− 20 = (2a − 2b)(6a + 2b) 5 = (a − b)(3a + b)

	2		10		9		3
5 =		a *		a ⇒ a2 =		⇒ a =
	3		3		4		2

	20
2a + 2a + 2a + 2b =		a = 10
	3

	2√3
h =		a = √3
	3

P = 5√3

Godzio: 9. Nie wiem czy tak można, ale najwyżej się poprawi log_ac + log_bc ≥ 4log_abc

	logabc		logabc
P =		+		=
	logaba		logabb

	logabc(logabb + logaba)
=		=
	logabb * logaba

	logabc
=
	logabb * logaba

logabc
	≥ 4logabc ⇔
logabb * logaba

log_abc^{log_b(ab) * log_a(ab)} ≥ log_abc⁴ ⇔ (log_ba + 1)(log_ab + 1) ≥ 4 ⇔

	1
(		+ 1)(logab + 1) ≥ 4 ⇔
	logba

	1
1 +		+ logab + 1 ≥ 4 ⇔ logba = t
	logba

1
	+ t ≥ 2 /* t2 ⇔
t

t + t³ ≥ 2t² ⇔ t³ − t² − t² + t ≥ 0 ⇔ t²(t − 1) − t(t − 1) ≥ 0 ⇔ (t − 1)² * t ≥ 0 log_ba < 0 log_ba < log_b1 a < 1 −− sprzeczne z założeniami Więc nierówność jest spełniona zawsze

Godzio: 10. Nie, przykładem takiego rosnącego ciągu z którego nie można wybrać ciągu geometrycznego jest ciąg liczb pierwszych

sssss: A sprobuj najprostszym sposobem rozwiazac takie : W trapezie o podstawach 2 i 1 przekatne sa do siebie prostopadle. Oblicz sume kwadratow przekatnych.

sssss: Mozesz tez wziac udzial w konkursie na politechnice warszawskiej : Www.sigma.mini.pw.edu.pl , tam sa ciekawe zadania.

bart:

	1
logba=		tutaj cos pokreciles
	logab

Godzio:

	1
Ale to tylko zapis reszta jest poprawna		, t = logab a dalej już tak jak tam jest
	logab

bart: a masz t=log_ba

Godzio: uwierz mi, wszystko jest dobrze wystarczy podmienić log_ba na log_ab bo z błędem przepisałem i jest ok

Eta: Godzio czemu w tym zad. ......... zapomniałeś o "moich średnich"

Godzio: Kolejne się udało

	α + β		tgα + tgβ		π
tg		<		0 < α < β <
	2		2		2

1 − cos(α + β)		sin(α + β)
	<
sin(α + β)		2cosαcosβ

1 − cos(α + β)		sin(α + β)
	<		⇔
sin(α + β)		cos(α − β) + cos(α + β)

(1 − cos(α + β))(cos(α − β) + cos(α + β)) < sin²(α + β) ⇔ cos(α − β) + cos(α + β) − cos(α + β)*cos(α − β) − cos²(α + β) < sin²(α + β) ⇔ cosαcosβ + sinαsinβ + cosαcosβ − sinαsinβ − cos²αcos²β + sin²αsin²β < 1 ⇔ 2cosαcosβ − cos²αcos²β + (1 − cos²α)(1 − cos²β) < 1 ⇔ 2cosαcosβ − cos²αcos²β + 1 − cos²β − cos²α + cos²αcos²β < 1 ⇔ 2cosαcosβ + 1 − cos²β − cos²α < 1 ⇔ −(cos²β − 2cosαcosβ + cos²α) < 0 (cosβ − cosα)² > 0 cosβ − cosα = x < 0 ⇒ x² > 0

Godzio: Eta, właściwie jakim zadaniu ? z logarytmami ? niezbyt tam to widzę

Bogdan: Witaj Godzio. Widzę, że z niektórymi zadaniami już kiedyś się zetknąłeś. Inne, mam nadzieję, dostarczyły Ci trochę emocji. Gratuluję pomysłowości i uporu Twoje rozwiązanie zadania z trapezem jest rzeczywiście proste, ale jest jeszcze prostsze rozwiązanie.

Godzio: Witaj Bogdanie, szczerze powiedziawszy tylko z 2 zadaniami się zetknąłem Skoro jest jeszcze prostszy to postaram się znaleźć jeszcze inne rozwiązanie

Bogdan: Przy rozwiązywaniu zadania najczęściej rozwiązujący próbuje dopasować do treści zadania jakiś znany sobie schemat, szablon, wzór, sposób, algorytm. To jest taka trochę bezmyślna metoda, czysto mechaniczna, nie ma w tym nic z twórczości. Szablon, wzór, umiejętność rachowania i przekształcania wyrażeń to tylko narzędzia, po które powinno się sięgać dopiero po obmyśleniu ścieżki prowadzącej do rozwiązania. Czasami trzeba zapomnieć o wszystkich metodach, schematach i wzorach, spojrzeć na zadanie bez obciążenia znaną sobie wiedzą i zabawić się w odkrywcę. Można przy okazji tworzenia rozwiązania otrzymać zupełnie nie znany algorytm, wzór. Gwarantowana przy takiej badawczej pracy satysfakcja i radość.

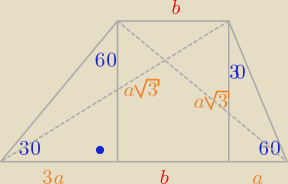
Godzio: Może w końcu to ten sposób będzie f² = h² + (3a + b)² e² = h² + (b + a)² 20 = (3a + b − b − a)(3a + b + b + a) 20 = 2a(4a + 2b)

	10
4a + 2b =
	a

	4a + 2b
P =		* a√3 = 5√3
	2

nasprawdzian: PS. https://matematykaszkolna.pl/forum/77667.html Prosze o szybkie wyjaśnienie. Z góry dziękuję.

Bogdan: No Godzio − jestem pod wrażeniem ostatniego rozwiązania zadania z trapezem. Jest super proste, ale można je rozwiązać jeszcze prościej. Zrezygnuj z różnych zastosowanych dotąd przez Ciebie schematów, np. z odejmowania stronami e² − f².

Godzio: Dzisiaj chyba jeszcze nie wymyślę jak inaczej obliczyć to pole, Bogdan mógłbyś pokazać jak zrobić to zadanie: Znajdź wszystkie liczby naturalne n takie, że liczby 5ⁿ − 2 i 5ⁿ + 2 są pierwsze. Domyślam się że n = 1 ⇒ 5 − 2 = 3, 5 + 2 = 7 i pewnie tylko dla tego jedynego n jest to spełnione ale jak uzasadnić że nie istnieje więcej takich n ?

b.: wypisz sobie więcej takich par i zobacz, czy obie liczby są pierwsze − i dlaczego nie może coś zauważysz...

Bogdan: i zauważ, że liczby 5ⁿ − 2, 5ⁿ, 5ⁿ + 2 to trzy kolejne liczby nieparzyste, wśród nich jest jedna podzielna przez 3, która?

Godzio: Wypisywałem sobie kilka tych liczb i rozbijałem, wyszło mi że 5ⁿ − 2 i 5ⁿ + 2 są na przemian podzielne przez 3 dla n nieparzystego 5ⁿ − 2 dzieli się przez 3, dla n parzystego 5ⁿ + 2 dzieli się przez 3 więc więcej takich par nie istnieje

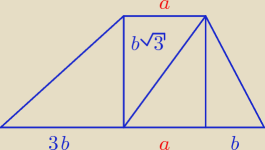
Godzio: Kolejny sposób

Godzio:

	4b + 2a
P =		* h
	2

	a + b
cosα =
	f

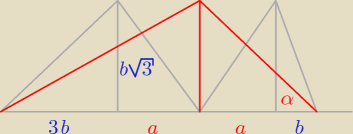
e² = f² + (4b + 2a)² − 2f(4b + 2a)cosα e² − f² = (4b + 2a)² − 2(4b + 2a)(a + b) 20 = (4b + 2a)(4b + 2a − 2a − 2b) 20 = (4b + 2a) * 2b

	4b + 2a
h = b√3 ⇒ 10√3 = (4b + 2a) * b√3 ⇒ 5√3 =		* b√3
	2