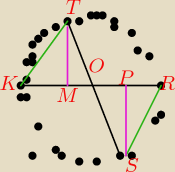
Geometria Ela: Wykaż, że odcinek MO = odcinkowi PO. Oczywiście ten rysunek to okrąg ze średnicą . Zadanie z pierwszej technikum.

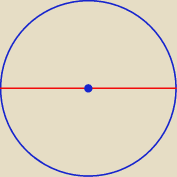
Bogdan: A tu są takie porządne narzędzia do rysowania. Co powiesz o odcinkach KT i RS ?

Ela: Są takiej samej dlugości...

Ela: Można też zauważyć kąty wierzchołkowe, no ale co dalej?

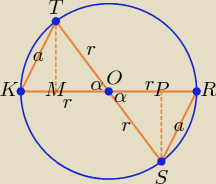
Bogdan: Czy trójkąty KOT i ROS są przystające? Odpowiedź na to pytanie ułatwi rozwiązanie zadania.

Bogdan: Które jeszcze trójkąty są tu przystające?

Ela: KOT i ROS są przystające z zasady bok−kąt−bok lub bok−bok−bok.

Bogdan: Czy przystające są także trójkąty TOM i ROS ?

Ela: Hmmm − mają ten sam kąt α, bok r i nic poza tym jak dla mnie, więc nie są przystające...

Bogdan: Przepraszam, poprawiam pytanie. Czy przystające są także trójkąty TOM i POS?

Konrad: bkb − r, kąt α i znowu r

Ela: Ale my nie wiemy czy punkt P i punkt M leżą w takich samych odległościach od O, a to na pewno nie ma wartości r... To właśnie należy udowodnić...

Ela: ?

Ela: Wiem, ze na rysunku to wszystko widac, ale jak uzasadnic to typowo matematycznie...?

Bogdan: Odcinki TM i PS są wysokościami trójkątów: KOT z podstawą KO i ROS z podstawą RO. Skoro trójkąty KOT i ROS są przystające, to odcinki TM i PS są równej długości i każdy z nich opada na swoją podstawę pod kątem prostym. Miary kątów: OTM i OSP w trójkątach prostokątnych TOM i POS są równe sobie i wynoszą 90^o − α. Ostatecznie |TM| = |PS| i |OT| = |OS| = r i |∡OTM| = |∡OSP|, więc trójkąty TOM i POS są przystające na podstawie cechy przystawania bkb. Stąd |MO| = |PO|.

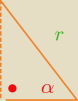
flare: mi sie wydaje ze tu jest kat prosty w jednym i drugim, alfa jest w obu, wiec trzeci kat jest taki sam, no i maja takie same boki r, wiec sa przystajace