Proszę o pomoc!!!
ola0912: W ostrosłupie prawidłowym czworokątnym kąt między przeciwległymi krawędziami bocznymi ma miarę
90 stopni. Przekątna podstawy ostrosłupa ma długość 5√2dm. Oblicz:
a) sumę długości wszystkich krawędzi tego ostrosłupa
b) miarę kąta zawartego między dwiema sąsiednimi krawędziami bocznymi ostrosłupa.
odpowiedzi są takie: a) 40 dm b) 60 stopni. Robiłam na różne sposoby i zawsze źle wychodzi.
1 lut 16:57
dero2005:
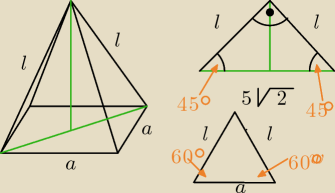
wg trójkąta w górnym prawym rogu
jeden kąt 90° wg treści zadania, czyli jest to trójkąt prostokątny równoramienny
pozostałe dwa kąty po 45°
l
2 + l
2 = (5
√2)
2
2l
2 = 50
l
2 = 25
l = 5
podstawa ostrosłupa
a
2 + a
2 = (5
√2)
2
2a
2 = 50
a
2 = 25
a = 5
wynika z tego, że krawędzie podstawy a są równe z krawędziami bocznymi, czyli
a = l = 5
ponieważ wszystkich krawędzi jest 8 to suma krawędzi jest równa
8*5 = 40 dm
zgodnie z tym, trójkąt ściany bocznej jest trójkątem równobocznym, którego kąty wynoszą po 60°
1 lut 17:51
juska: wysokość prawidłowego ostrosłupa sześciokątnego jest równa5{3}cz, a kąt między przeciwległymi
krawędziami bocznymi ma 60*. Oblicz sumę długości wszystkich krawędzi tego ostrosłupa.
5 gru 20:00
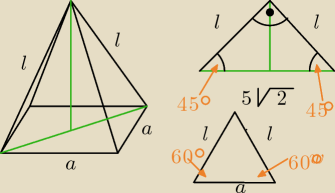 wg trójkąta w górnym prawym rogu
jeden kąt 90° wg treści zadania, czyli jest to trójkąt prostokątny równoramienny
pozostałe dwa kąty po 45°
l2 + l2 = (5√2)2
2l2 = 50
l2 = 25
l = 5
podstawa ostrosłupa
a2 + a2 = (5√2)2
2a2 = 50
a2 = 25
a = 5
wynika z tego, że krawędzie podstawy a są równe z krawędziami bocznymi, czyli
a = l = 5
ponieważ wszystkich krawędzi jest 8 to suma krawędzi jest równa
8*5 = 40 dm
zgodnie z tym, trójkąt ściany bocznej jest trójkątem równobocznym, którego kąty wynoszą po 60°
wg trójkąta w górnym prawym rogu
jeden kąt 90° wg treści zadania, czyli jest to trójkąt prostokątny równoramienny
pozostałe dwa kąty po 45°
l2 + l2 = (5√2)2
2l2 = 50
l2 = 25
l = 5
podstawa ostrosłupa
a2 + a2 = (5√2)2
2a2 = 50
a2 = 25
a = 5
wynika z tego, że krawędzie podstawy a są równe z krawędziami bocznymi, czyli
a = l = 5
ponieważ wszystkich krawędzi jest 8 to suma krawędzi jest równa
8*5 = 40 dm
zgodnie z tym, trójkąt ściany bocznej jest trójkątem równobocznym, którego kąty wynoszą po 60°