awdawdawdaw awdwdawda: Wyznacz prostą równoległa i prostopadłą przechodzące przez punkt C (4,5). Prosta przechodzi przez punkt A(−3,−5) B(−3,2) Rozumiem wynik. Prostopadła y=5, równoległa x=4 Jednak to jakiego wzorru zostało to podstawione i policzone? W jaki sposób ?

awdwdawda:

awdwdawda:

karolajn:

karolajn:

Bogdan: Jeśli prosta przechodzi przez punkty A(x₁, y₁) i B(x₂, y₂), to: 1) dla x₁ ≠ x₂ obliczamy współczynnik kierunkowy a z zależności:

	y1 − y2		y2 − y1
a =		względnie a =
	x1 − x2		x2 − x1

Prosta ma równanie: y = a(x − x₀) + y₀, gdzie x₀, y₀ to współrzędne punktu A lub B. 2) dla x₁ = x₂ i y₁ ≠ y₂ prosta jest równoległa do osi y i ma równanie: x = x₁ 3) dla x₁ ≠ x₂ i y₁ = y₂ prosta jest równoległa do osi x i ma równanie: y = y₁.

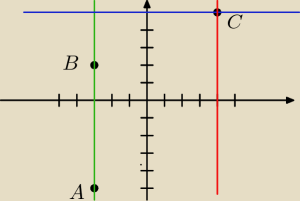
dero2005: prosta przechodząca przez punkty A i B (x₂−x₁)(y−y₁) = (y₂−y₁)(x−x₁) (−3+3)(y+5) = (2+5)(x+3) 0(y+5) = 7(x+3) 0 = 7x+21 7x = −21 x = −3 równoległa przechodząca przez punkt C(4, 5) x = 4 prostopadła y = 5

Gustlik: Dero, szczerze mówiąc, ja siędzę w matmie od bardzo dawna, ale chcąc korzystać z tego długiego jak tasiemiec wzoru musiałbym go sobie albo za każdym razem wyprowadzać, albo za każdym razem tracić czas na szukanie go w tablicach i jeszcze uważać, żeby nie podstawić błędnie współrzędnych. A przecież ten wzór wziął się z wzoru Bogdana:

	y2−y1
a=
	x2−x1

Do tego wzór y=ax+b i nie potrzeba żadnych ciężko strawnych tasiemców z czterema nawiasami. Zdecydowanie polecam metodę Bogdana.