Funkcja trygonometryczna kąta ostrego.

Funkcja trygonometryczna kąta ostrego. niunia15xD: Długość przekątnych rombu wynoszą d₁ = 6 cm oraz d₂ = 2√3 cm. Oblicz długość boku rombu oraz miarę kąta ostrego zawartego między bokami.

1 lut 00:15

Bogdan: a znasz twierdzenie Pitagorasa?

1 lut 00:17

kachamacha: powstaje Δ prostokątny o przyprostokątnych 3 i √3 (połowy przekątnych) i przeciwprostokątnej a−bok rombu wykorzystaj twierdzenie Pitagorasa

1 lut 00:19

Mentosik : przekątne rombu dzielą go na 4 trójkąty prostokątne, gdzie każdy z trójkątów ma przyprostokątne o wymiarach 3cm i √3 z tw. Pitagorasa: a − bok rombu a² = 3² + √3² a² = 12 a = 2√3 zaraz podam kąt

1 lut 00:21

Bogdan: Idziemy kachamacha ramię w ramię emotka

1 lut 00:21

kachamacha:

1 lut 00:22

kachamacha: 60^o

1 lut 00:27

Mentosik : kąt alfa zaznaczasz w trójkącie prostokątnym między prostokątną o wymiarze 3 a przeciwprostokątną, bo tam jest mniejszy kąt sin alfa = √3 / 2√3 = 1/2 a to jest 30 stopni zatem kąt rombu jest 2 razy większy (przekątna była dwusieczną kąta ostrego), czyli 60 st. sorki że tak wolno, szukałem tablicy z wartościami, choć niepotrzebnie

1 lut 00:29

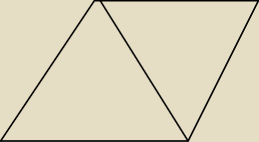
kachamacha: wystarczy zauważyć Δ równoboczny

1 lut 00:35

kachamacha: rysunek

{

1 lut 00:38

kachamacha: z krótszą przekątną mamy Δ równoboczny

1 lut 00:38