Andrzej Kiełbasa Funkcja Liniowa Jeruzalem: 132. Dla jakich wartości parametru a równanie |x−2|=a² −3a−2 ma dwa pierwiastki różnych znaków Odp. (−∞;−1)U(4;+∞) 134. Rozwiąż równanie a²(x−1)−ab=b²(x+1)+ab gdzie a i b są parametrami. Do tego zadania tylko pytanie: Doszedłem do momentu x(a²−b²)=(a+b)² i jeżeli podzielę obie strony przez (a²−b²) to równanie ma jedno rozwiązanie, natomiast jak sprawdzić kiedy równanie ma nieskończenie wiele rozwiązań albo ich nie ma wcale. To się robi na tym etapie? I czy polega to na metodzie podstawiania liczby i sprawdzania ? Dzięki za pomoc

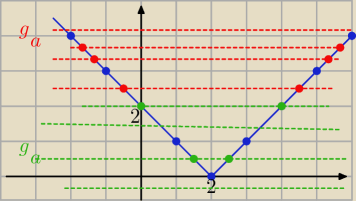
Eta: Rysując wykres f(x)= |x−2| zauważamy,że równanie będzie mieć dwa rozwiązania różnych znaków wtedy gdy prosta y= g(a) przetnie ten wykres w I i II ćw. układu współrzędnych czyli powyżej wartości y= 2 zatem ten warunek będzie spełniony dla: g(a) >2 a²−3a −2 >2 rozwiąż tę nierówność i podaj przedziały do,których należy "a"

utan: nieskończenie wiele rozwiązań, gdy 0x = 0 czyli { a² − b² = 0 { (a+b)² = 0 brak rozwiązań, gdy { a² − b² = 0 { (a+b)² ≠ 0 jedno rozwiązanie, gdy { a² − b² ≠ 0 (wtedy ci wolno dopiero podzielić, stąd jedno będzie rozwiązanie)

Jeruzalem: Dzieki wam