Wyznacz długość wysokości trójkąta równoramiennego Damian: Wyznacz długość wysokości trójkąta równoramiennego o wierzchołkach A=2, −5); B=(−4,2); C=(4,4)

M:

M:

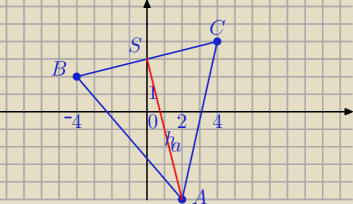
Mila: A=(2, −5); B=(−4,2); C=(4,4) 1) |AB|=√6²+7²=P{36+49}=√85 |BC|=√8²+2²=√68 |AC|=√2²+9²=√85=|AB|

	2+4
S− Środek BC: S=(U{{−4+4}{2},		=(0,3)
	2

Prosta BC: 2) y=ax+3 i C∊ BC

	1
y=		x+3⇔4y=x+12
	4

x−4y+12=0

	|2−4*(−5)+12|
ha=D(A,BC)=
	√1+16

	34
ha=
	√17

3)

	1		1		34
PΔ=		*|BC|*ha=		√68*		=34
	2		2		√17

	1
34=		*√85*hb /*√85
	2

64√85=85h_b

	64√85		4√85
hb=		=		=hc
	85		5

Leszek: h_a = |AS| = √(2−0)² + (−5−3)² = 2√17 , można tak .

Mila: Tak , to lepszy sposób