BANAŁ :) t.: BANAŁ NA 5 minut zad.1 Oblicz kąty trójkąta równoramiennego ABC, w którym |AC|=|BC|, a dwusieczna AD tworzy z bokiem BC kąt 120°. podam odpowiedzi: 40,40,100 badz 80,20,20. Dziekuje z gory

t.: pomoze ktos ?

t.:

ancymon:

t.: nikt..?

t.: co to jest?

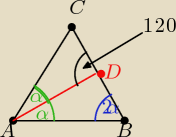
utan: druga odp podana przez Ciebie jest zła, powinno być 80, 80, 20 kąt przy A = 2α kąt przy B = 2α kąt przy C = 180 − 4α z trójkąta ADC α + 120 + 180 − 4α = 180 −3α = −120 α = 40 kąt przy A = 2α = 2*40 = 80 kąt przy B = 2α = 2*40 = 80 kąt przy C = 180 − 4*40 = 20 druga opcja wychodzi, gdy 120 stopni dasz w ADB

t.: masz racje,spiacy juz jestem ledwo co pisze glowa nie mysli a na dodatek miami grac z oklahoma i jestem nie ogarniety dzieki wielkie.

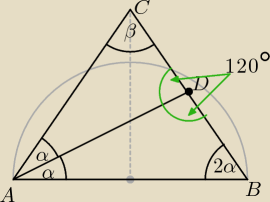
think: są dwie opcje położenia kąta 120 stopni. Równoramienny trójkąt ma takie same kąty między ramieniem a podstawą. 2α + 2α + β = 180 ⇒ β = 180 − 4α teraz masz dwa przypadki I gdy 120 stopni jest w trójkącie ADC α + β + 120 = 180 II gdy 120 stopni jest w trójkącie ADB α + 2α + 120 = 180 wylicz jakie będą możliwe kąty.

t.: a czego tam wzioles 180 − 4α ? mozna tak wierzcholek wyliczac odejmujac 2 inne wierzcholki ?

think: to nie wierzchołki tylko miary kątów... suma kątów w trójkącie wynosi 180 stopni. I owszem można tak odejmować, takie odejmowanie ma swoje korzenie w metodzie rozwiązywania układów równań metodą podstawienia I nie czego tylko proszę a tak na marginesie jak już to wzięłam...

t.: czyli bedzie α+120+180−4α=180 −3α=−120/:−3 α=40 wychodzi 80,80,20 2 przypadek: α+120+2α=180 3α=60/:3 α=20 wychodzi:40,40,100 dzieki wielkie co ja bym zrobil bez tej strony i takich ludzi.nie licze ze ktos mi rozwiaze i spisze do zeszytu , wazna jest nauka i chec jej poglebiania.

think: no to się cieszę, że mogłam pomóc

Karolka: O pewnym trójkącie wiadomo, że dwusieczne dwóch jego kątów zawierają wysokości tego trójkąta. Jaki to trójkąt ?