. Kejt: Do Godzia Mógłbyś w wolnej chwili wytłumaczyć mi to zadanie? Dla jakich wartości parametru m równanie (1+m)x²−3mx+4m=0 posiada dwa pierwiastki, z których jeden jest większy, a drugi mniejszy od liczby 1? zaczęłam tak: Δ>0 Δ=9m²−4(1+m)*4m=9m²−16m−16m²=−7m²−16m −7m²−16m>0 −m(7m+16)>0 −m=0 m=0 7m+16=0 7m=−16

	16
m=−
	7

	16
m∊(−		;0)
	7

co dalej? w Twoim rozwiązaniu się pogubiłam..

Trivial: Czy Godzio ma monopol na tłumaczenie zadań z parametrem?

Eta:

Kejt: nie, po prostu to zadanie jest od niego i już je rozwiązywał. jak chcesz to możesz mi potłumaczyć

Bogdan: Jeśli liczba r∊(x₁, x₂), gdzie x₁, x₂ to pierwiastki równania ax² + bx + c = 0, to przyjmujemy założenia: (1) a ≠ 0 (2) Δ > 0 (3) a*f(r) < 0 Do odpowiedzi bierzemy część wspólną przedziałów będących rozwiązaniami tych trzech nierówności.

Kejt: hmm.. może to będzie głupie pytanie, ale zaryzykuję. skąd wynika ostatnie założenie?

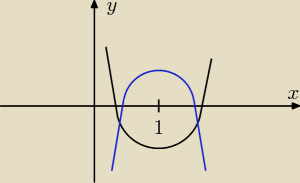
Godzio: Mamy 2 takie sytuacje, oczywiście Δ > 0 Pierwsza sytuacja a < 0 wartość dla 1 musi być większa od zera ⇒ f(1) > 0 Druga sytuacja: a > 0 wartość dla 1 musi być mniejsza od zera ⇒ f(1) < 0 Bogdan zastąpił te 2 przypadki jednym: a * f(1) < 0 Gdybyś nie chciała tego tak rozwiązywać to proponuję tak: 1^o Część wspólna z:

⎧	Δ > 0
⎨	a < 0
⎩	f(1) > 0

2^o Część wspólna z:

⎧	Δ > 0
⎨	a > 0
⎩	f(1) < 0

Odp: Suma rozwiązań z 1^o i 2^o

Godzio: To są zadania z funkcji kwadratowej w których nie trzeba wykorzystywać wzorów Viet'a, Trzeba narysować sobie sytuację która nas interesuje i zobaczyć jakie założenia są potrzebne aby warunki zadania były spełnione

Kejt: już wszystko jasne, dziękuję bardzo