funkcja odwrotna i zbior wartosci niedoswiadczona matematyczka: Funkcja f:R→R dana jest wzorem f(x)=π−2arctg(x). Wówczas: a) zbiór wartości funkcji f,Y= b) Funkcja odwrotna f⁻¹: Y→R dana jest wzorem f⁻¹(x) Prosiłabym o pomoc w tym zadaniu

niedoswiadczona matematyczka: Według mnie Y= <0, 2π>.. mam rację?

niedoswiadczona matematyczka:

	x−π
A funkcja odwrotna y=sin(		). Tak? Pomóźcie...
	−2

niedoswiadczona matematyczka: Prosze powiedzcie czy mam chociaz ja dobrze..

laxit: o ja też miałem to zadanie na egzaminie czyzby ekonomia na UG? dołaczam się też do tego zadania prosząc o rozwiązanie

laxit: odnawiam temat...

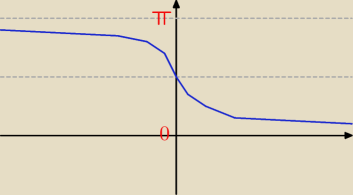
Bogdan: y = π − 2arctgx (wykres na rysunku) Y: y∊(0, π) Wyznaczenie wzoru funkcji odwrotnej. Funkcja f(x) = π − 2arctgx jest różnowartościowa.

	π		1
y = π − 2arctgx ⇒ 2arctgx = π − y ⇒ arctgx =		−		y
	2		2

	π		1		1
x = tg(		−		y) ⇒ x = ctg(		y)
	2		2		2

	1
y = ctg(		x)
	2

	x
f−1(x) = ctg(		)
	2

laxit: hmm ale wykres nie powinien być rozciągniety bo sprzodu arctgx jest 2 i przesuniety do góry o π?

Bogdan: Tak, chochlik znowu namieszał, powinno być 2π

Bogdan: Poprawiam zbiór wartości funkcji: y∊(0, 2π), źle przepisałem z mojej kartki, dziękuję laxit za zwrócenie uwagi.

laxit:

	π
a czemu tam w czasie przekształcania znikło
	2

think: laxit, pewnie ma to coś wspólnego z cudowną przemianą tg na ctg jakieś wzory redukcyjne