mat nieznajoma_88: W trójkącie równoramiennym ABC dane są wierzchołki podstawy A=(1,0) i B=(−3,2) Pole tego trójkąta równa się 5. Wyznacz współrzędne wierzchołka C.

ICSP: No więc według mnie: Liczysz długość podstawy ze wzoru na długość odcinka. Wyznaczasz środek odcinka AB Wyznaczasz równanie prostej podstawy wyznaczasz równanie prostej prostopadłej do prostej AB przechodzącej przez punkt s który jest środkiem odcinka AB Sprawdzasz jaka jest odległość punktu C od podstawy(pole trójkąta). Układasz układ równań i znajdujesz współrzędne punktu C(będą dwa takie punkty)

nieznajoma_88: tak zrobiłam tylko: 5x² + 10x <= taki wynik i nie jestem pewna bo z pierwiastkami raczej nie

ICSP: to nie są współrzędne...

nieznajoma_88: Przeciez wiem jak z tego obliczyć x₁ i x₂ tylko nie wiem czy to poprawne równanie. Wszystko tak samo jak ty zrobiłam.

nieznajoma_88: Może podam jakie mam funkcje liniowe:

	1		1
AB −> y = −		x +
	2		2

CS −> y = 2x + 3

nieznajoma_88: Sprawdzi ktoś?

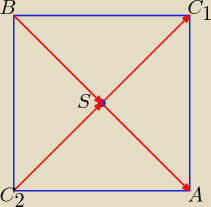
Bogdan: Po ustaleniu, że AC₁BC₂ jest kwadratem, można zagonić do roboty wektory, znacznie upraszczają rozwiązanie zadania. A = (1, 0), B = (−3, 2), S = (−1, 1) → → → → BS = [2, −1], C₂S = SC₁ = [1, 2], −C₂S = [−1, −2] C₁ = (−1 + 1, 1 + 2) = (0,3), C₂ = (−1 − 1, 1 − 2) = (−2, −1)

ICSP: Dobrze.

nieznajoma_88: A mógłbyś zrobić bez wektorów? Tak jak ja robiłam? Tak jak pisałam:

	1		1
AB −> y = −		x +
	2		2

CS −> y = 2x + 3 Odległość AB to 2√5 S = (−1,1)

	1
P =		ah
	2

5 = √5h /:√5 h = √5 i teraz: √5 = √(−1−x)² + (1−y)² /:()² 5 = (−1−x)² + (1−y)² po podstawieniu za y= 2x+3 otrzymuje 5x²+10x = 0 i coś mi tu nie gra

Bogdan: gra , 5x² + 10x = 0 ⇒ 5x(x + 2) = 0 ⇒ x = 0 lub x = −2

nieznajoma_88: Ahh, faktycznie Zapomniałam: że c = 0 Δ = b² − 4ac Δ = 100 − 4*5*0 √Δ = 10

	−10−10
x1 =		= −2
	10

	−10+10
x2 =		= 0
	10

y₁ = 2(−2) + 3 => −1 y₂ = 2 * 0 + 3 => 3 Już gra THX

Bogdan: ale bez Δ rozwiązuje się równania kwadratowe niezupełne

nieznajoma_88: wiem wiem i to był mój błąd bo nie zauwazyłam ze nie ma c