Wyznacz ekstrema Bjornolf: f(x)=x e^−2x Zaciąłem się przy f'(x)=0 Z góry dziękuję za pomoc, Pozdrawiam

Bogdan: to podaj swoją pochodną

Bjornolf: problem leży w tym, że mi, "na oko", wychodzi nielogiczna. t=−2x t'=−2 f'(x)=e^−2x+xe^t t' =e^−2x−2xe^−2x=e⁻²(1−2x) (e^t)'= e^t ? wiec teraz rozwiązuję 1−2x=0 ?

Bjornolf: w końcowym wyniku e^−2x(1−2x) miałem napisać

Bogdan:

	1
f'(x) = −2e−2x(x −		), e−2x > 0 dla każdej wartości x∊R
	2

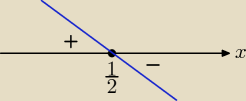
Pochodna zmienia znak przy przejściu przez punkt x = U[1}{2} z plus na minus,

	1		1
więc w punkcie x =		funkcja posiada maksimum równe f(		).
	2		2

Bogdan:

	1
Pochodna zmienia znak przy przejściu przez punkt x =		z plus na minus ...
	2

Bjornolf: dziękuję