Twierdzenie cosinusów Maturzystka: W okrąg o promieniu 1, wpisano trójkąt o bokach długości a, b i c. Wykaż, że trójkąt ten jest ostrokątny gdy a²+b²+c²>8

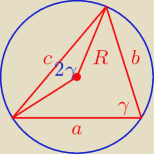
Godzio: Z tw. cosinusów: c² = 2 − 2cos2γ Trójkąt jest ostrokątny tylko wtedy gdy: a² + b² > c² / + c² ⇒ a² + b² + c² > 2c² = 4 − 4cos2γ = 4(1 − cos²γ + sin²γ) = 8sin²γ 0 ≤ sin²γ ≤ 1 więc a² + b² + c² > 8sin²γ ≤ 8 co kończy dowód, Mógłby ktoś jeszcze na to zerknąć czy nie ma błędu w rozumowaniu ?

Maturzystka: a² + b² + c² > 8sin2γ ≤ 8 co kończy dowód, Nie za bardzo rozumiem tego stwierdzenia przecież 8 nie musi być wtedy mniejsze od prawej strony a więc nie jest to udowodnione

Basia: 1. Maturzystka ma niestety rację, to nie kończy dowodu 2. Jak właściwie brzmi twierdzenie ? Jeżeli jest ostrokątny ⇒ a²+b²+c² > 8 czy odwrotnie Jeżeli a²+b²+c²>8 ⇒ jest ostrokątny

Basia: moim zdaniem chodzi o to niebieskie przypuśćmy, że jeden z kątów np. γ≥90 (γ oczywiście <180) wtedy 0 < α,β < 90 i mamy a² = 2−2cos2α b² = 2−2cos2β c² = 2−2cos(360−2γ) = 2−2cos2γ i mamy 0 < cosα,cosβ < 1 −1< cosγ ≤ 0 /*(−2) 2 > −2cosγ ≥ 0 /+2 4 > 2−2cosγ≥ 2 2 ≤ c² <4 czyli a²<2 b²<2 c²<4 czyli a²+b²+c² < 2+2+4 = 8 sprzeczność czyli γ nie może być kątem rozwartym co kończy dowód

Basia: korekta: czyli γ nie może być kątem rozwartym ani prostym co kończy dowód Twierdzenia "w drugą stronę" (czerwonego) nie umiem na razie ani udowodnić, ani obalić.

Godzio: Aha, czyli ja zrobiłem że jeżeli jest ostrokątny to spełnia ten warunek ?

Basia: tak, ale na końcu jest błąd; ten, o którym pisze Maturzystka a² + b² + c² > 8sin2γ ≤ 8 co kończy dowód, to prawda, ale to nie dowodzi, że a²+b²+c²>8 (nierówność nie w tę stronę)

Godzio: Ok, rozumiem

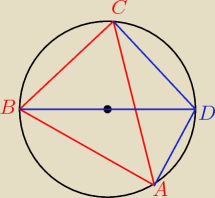
Basia: W drugą stronę to proste jak budowa cepa BD = 2 BC²+CD²=4 AB²+AD²=4 AB²+BC²+AD²+CD²=8 ∡B jest ostry ⇒ ∡D jest rozwarty ⇒ AC²=AD²+CD² − 2*AD*CD*cos∡D > AD²+CD² AB²+BC²+AC² > AB²+BC²+AD²+CD² = 8