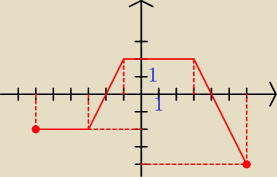
Andrzej Kiełbasa Funkcje str 36 Jeruzalem: 112.(rysunek) Obok zamieszczono wykres funkcji f. Funkcja g określona jest w następujący sposób g(x) = |f(x−1)+2| c) Podaj zbiór rozwiązań nierówności g(x) ≤ 2x + 4 Odp . <−2;7> 113. Wykres funkcji f(x) = U{x−3}{x²−x−6{ przesunięto o wektor [−2,1],a nastepnie przesunięty wykres odbito symetrycznie względem początku układu współrzędnych. Otrzymano wykres pewnej funkcji g. Znajdź wzór i wyznacz dziedzinę funkcji g.

	−x2 + 4x + 5
Odp. g(x) =		, dziedzina R \ {−1,4}
	x2 − 3x − 4

	x2+4x+5
115. Funkcja f określona jest wzorem f(x)=		. Wykres funkcji f przesunięto o
	x2+4x

wektor [p;0], otrzymując wykres funkcji g. Znajdź wzór funkcji g i współrzędne wektora wiedząc że wykres funkcji g jest symetryczny względem osi OY

	x2 + 1
Odp. wektor [2;0], g(x) =
	x2 − 4

117. Funkcja f określona w zbiorze R, jest malejąca. Funkcja g dla każdej liczby rzeczywistej x określa równość g(x) = f(x³ − 3x) a) Która liczba jest większa f(−1) czy g(1)? Odp. g(1) > f(−1) Możecie zrobić kiedy wam będzie pasowało Z Góry dzięki

think: f(x − 1) + 2 mówi, że ten wykres masz przesunąć o 1 jednostkę w prawo i 2 jednostki do góry nałożona na to wartość bezwzględna dodaje, że masz po tym przesunięciu jeszcze odbić nad oś x−ów wszystko co pod osią zostało po dokonaniu przesunięcia. jak masz już rysunek to rysujesz sobie prostą y = 2x + 4 i sprawdzasz kiedy wykres funkcji g(x) jest pod wykresem y = 2x + 4 lub się z nim przecina.

Jeruzalem: o kurcze tylko tyle heh dzięki

think: co do 113 najpierw przesunięcie o wektor [−2,1] funkcji f(x) wygląda tak g(x) = f(x + 2) + 1 teraz trzeba g(x) odbić względem OX i OY czyli −g(x) powoduje odbicie jej do góry nogami względem OX a −g(−x) to już odbite względem OX jest odbite względem OY.

think: w zad 115, już sam możesz zapisać jak wygląda przesunięcie o wektor, na podstawie tych dwóch wcześniejszych zadanek. Co do symetrii względem OY to warunek, że g(x) = g(−x)

think: co do 117 to zapisz sobie jaki jest warunek na to aby funkcja była malejąca, wiesz dla rosnących argumentów jak się zachowują wartości funkcji.

Jeruzalem:

	x
kurcze co do 113 wyszło mi takie coś i nie wiem co dalej z tym zrobić y =
	x2−3x−3

think:

	x − 3
f(x) =
	x2 − x − 6

h(x) = f(x +2) + 1

	(x + 2) − 3
h(x) =		+ 1
	(x + 2)2 − (x + 2) − 6

g(x) = −h(−x)

think: no to policz jeszcze raz.

Jeruzalem: no tak źle tą jedynkę podstawiłem dziekuje bardzo

Jeruzalem:

	x2 − 4x + 5
kurcze te 15 właśnie tak robiłem wyszlo mi y=		i nie wiem co dalej
	x2 − 4x

think: no to zajmijmy się samym tylko mianownikiem... (x + 2)² − (x + 2) − 6 = x² + 4x + 4 − x − 2 − 6 = x² + 3x − 4

Jeruzalem: O zadanie 115 mi chodziło

think: ups, człowiek już widzi to co chce widzieć...

	x2 + 4x + 5
f(x) =
	x2 + 4x

zapisz jak wygląda przesunięcie funkcji f(x) o wektor [p,0] chcę zobaczyć czy dobrze zapisałeś

Jeruzalem: własnie nie wiem czy będzie x+p czy x−p nie wiem jak to zapisać

think: ano właśnie o to chodzi.... przesunięcie funkcji f(x) o wektor [a,b] f(x − a) + b czyli np przesunięcie o [−5,2] wygląda f(x + 5) + 2

Jeruzalem: aa czyli pod p na pewno jest liczba dodatnia ?

Jeruzalem: skoro tak to f(x − p) + 0

think: hehehe jesteś w błędzie ale na liczbach ogólnych czyli m,a,x,c to nie ma znaczenia ten minus we wzorze jest zawsze, gdy masz już konkretne liczby to już robi różnicę. Dowód: p − dowolna liczba przesunięcie o wektor [p, 0] f(x − p) dla przykładowo f(x) = x² f(x − p) = (x − p)² = x² − 2px + p² gdyby p = 2 to f(x − 2) = x² − 2*2x + 2² = x² − 4x + 4 gdyby p = −2 działa ten sam wzór x² − 2*(−2)x + (−2)² = x² + 4x + 4 = (x + 2)² = f(x + 2) = f(x − (−2))

Jeruzalem: czyli pod wzór po prostu podstawić x−p ?

think: tak p może być dodatnie jak i ujemne jeszcze nic na ten temat nie wiemy.

Jeruzalem: ok to podstawie i powiesz co dalej

Jeruzalem:

	(x−p)2 + 4(x−p) + 5
f(x−p)=
	(x−p)2 + 4(x−p)

Jeruzalem: potem będzie zmiana znaków i to wszystko ?

think: nieee musisz to wymnożyć

	x2 + x(coś w nawiasie) + wyraz wolny
zapisać jako
	x2 + x(coś w nawiasie) + wyraz wolny

i teraz najważniejsze g(x) = g(−x) kiedy taki warunek zajdzie

Jeruzalem: p to jest jakiś parametr ?

think: tak

think: konkretnie parametr który masz wyznaczyć.

Jeruzalem: ciężki chleb kurcze think rozwiązal bys mi to wezme se to do serca

think: ocipiałeś... pierwsze primo to jest proste, drugie primo jestem dziewczyną więc nie rozwiązał....

think:

Jeruzalem: doszedłem do czegoś takiego licznik x²−x(2p+4) + p² − 4p + 5 hmmm nic mi to nie mówi

Jeruzalem: nie wiedziałem że dziewczyną jestes to daj mi jeszce jakąś wzkazówke nie dojde do tego

Jeruzalem: zaczynasz żałować że sie zgodziłaś co ?

think: nie zgadza się coś w liczniku, przekłamałeś gdzieś w znaku.

think: hehehe, co do żałowania, to zawsze mogę Cię przycisnąć tak żebyś to Ty żałował

Jeruzalem: przyciskaj ile chesz byle żebym zrozumiał

think: co Ci jeszcze w tym zadaniu mogę powiedzieć... jak będziesz miał g(x) poprawnie wyznaczone i g(−x) to przyrównasz to tak, że licznik ma się równać licznikowi a mianownik mianownikowi, z tego wyjdzie rozwiązanie

Jeruzalem:

(x−p)2+4(x−p)+5		(x+p)2−4(x+p)+5
	=
(x−p)2+4(x−p)		(x+p)2−4(x+p)

think: źle

Jeruzalem: dobra przespie sie z tym już nie męcze btw dzięki za pomoc

think:

	(x − p)2 + (4x − p) + 5
g(x) =		=
	(x − p)2 + 4(x − p)

x2 + x(4 − 2p) + p2 − p + 5
x2 + x(4 − 2p) + p2 − 4p

	(−x)2 − x(4 − 2p) + p2 − p + 5
g(−x) =
	(−x)2 − x(4 − 2p) + p2 − 4p

g(x) = g(−x) ⇔ x² + x(4 − 2p) + p² − p + 5 = (−x)² − x(4 − 2p) + p² − p + 5 i x² + x(4 − 2p) + p² − 4p = (−x)² − x(4 − 2p) + p² − 4p ⇔ x(4 − 2p) = −x(4 − 2p)

think: ano proszę, robisz błędy w znakach, nie wiem czy to efekt zmęczenia, czy na ogół masz z tym problem, musisz bardziej zwracać uwagę na to co robisz i jak.

Jeruzalem: ehh dzięki

Jeruzalem: chyba zmęczenie od 3 dni śpie po 4h

think: to w takim razie chyba pora się wyspać dobrej nocy

oooo: mmmmmmmmmmmmmmmmmm,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,