z pinokio: oblicz asymptoty pozioma i pionome 1 −−−−−−− e^x−1

pinokio: wyszlo mi pozioma 0 w + i −∞ i piowej brak?

think: pinokio a kiedy e^x − 1 = 0? bo wtedy masz pionową

pinokio: ln1?

pinokio: x=∞?

pinokio: nei wiem

pinokio:

think: no ln1 = ... ?

pinokio: czyli 0?

think: tak czyli masz asymptotę pionową x = 0

pinokio: a nie ma byc czasem jak licze w as.pionowej wyjsc + albo −∞

pinokio: lim = − + ∞ x−>x₀

pinokio: kurde nie ogarniam tego

think: owszem teraz powinieneś policzyć takie dwie granice:

	1
limx−>0−		= .....
	ex − 1

	1
limx−>0+		= .....
	ex − 1

gdybyś nie wiedział to są granice prawo i lewostronne.

pinokio: no wlasnie i nie wyszlo mi z nich ani ∞ ani −∞

think: już Ci tłumaczę, jest algorytm szukania asymptot. asymptota pionowa mamy z nią do czynienia w punktach wyrzuconych z dziedziny czyli np dla

	1
		takim punktem jest 0. Gdy już masz takie pojedyncze punkty to liczysz granice lewo i
	x

prawostronne aby zobaczyć jak ta funkcja i z której strony się do tej asymptoty zbliża. asymptota ukośna ze wzorów asymptota pozioma liczyć granice lim_+/−∞f(x) jeśli z takiej granicy wyjdzie wartość liczbowa masz asymptotę poziomą

pinokio: a sorry 1/0 to ∞!?

pinokio: ok dizeki wielkie

pinokio: czyli mam asymtote pionowa w 0 tak?

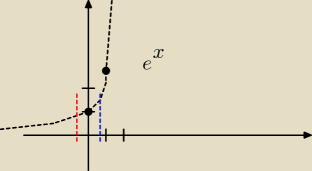
think: a właśnie że wyszło nie rozumiesz idei granicy lewo i prawostronnej. granica lewostronna czyli ten kawałek za czerwoną pionową krechą. jeśli x→0 to e^x → 1 ale nie osiąga, przyjmuje wartość bliską 1 ale mniejszą, np 0,999

	1		1
teraz liczysz wartość funkcji		=		→ −10000 a teraz gdybyśmy wybrali
	ex − 1		0,999 − 1

0,99999999... → −∞ natomiast gdy x dąży do 0 z lewej strony czyli od strony niebieskiej pionowej kreski, to e^x przyjmuje wartość większą od 1 np 1,000000000001

	1
i wtedy		→ +∞
	ex − 1

pinokio: aa spoko dzieki bardzo ze chce Ci sie tak tlumaczyc

pinokio: https://matematykaszkolna.pl/forum/76845.html

pinokio: czaisz?