Oblicz objętość i pole ostrosłupa prawidłowego sześciokątnego martina: Krawędź podstawy ostrosłupa prawidłowego sześciokątnego ma długość 2cm, a krawędź boczna 4cm.Oblicz objętość i pole powierzchni.

coco: Witam! napisz mi wzór na pole trójkata równobocznego! czekam! Razem rozwiążemy to zadanko! Chcesz tak ?

martina: P=a²√3:4 powinno być zapisane z kreską ułamkową ale nie bardzo wiem jak

coco: Pięknie! teraz jak obliczysz pole sześciokata foremnego? napewno tez wiesz? napisz mi może byc słoanie! OK? czekam !

martina: 6a²√3:4

coco: świetnie! To co? rozwiazujemy dalej ?

martina: no raczej tak dobrze,że po kolei robisz ze mną.Dzięki temu będę wiedzieć na przyszłość

coco: Podstaw za a = 2 i już mamy pole podstawy! pozostaje obliczyć H -- ostrosłupa tak? narysuj go to zobaczysz,że trójkat prostokatny gdzie jest H i k -- krawędź boczna ostr. i a bok trójkąta w tym sześciokącie z tw. Pitagorasa oblicz H h² = k² - a² k= 4 a= 2 więc już obliczysz H napisz ile wynosi to H ok? czekam!

coco: Właśnie o to chodzi żeby to rozumiec a nie gotowca przepisać! Po to tu jestem by Wam raczej wytłumaczyć!

martina: tak też wcześniej robiłam... czyli z moją matematyką nie jest tak źle jak myślałam... więc H=4√3? te pierwiastki są moją zmorą

coco: H= 2√3 więc masz błąd! bo zobacz H² = 16 -4 = 12 to H= √12 = √4*3 = 2√3 tak ?

martina: tak też myślałam,ale jak zwykle w mojej głowie się zapaliło błędne światło... a teraz wszystko jasne przecież 2² to 4 a √3² to 3 czyli 4*3=12....

coco: czyli dalej napisz wzór na V ostrosłupa! i podstaw te dane i napisz ile wyszło V

martina: V=1/3Pp*H V=1/3*4*2√3 V=1 1/3*2√3 ?

martina: ale to jest sześciokątny sorreczka

martina: V=1/3*6a²*2√3 V=8*2√3 tak? wersja po poprawce

coco: teraz pole ! najpierw obliczymy pole jednej ściany , która jes trójkątem równoraniennym o ramionach "k" i podstawie "a" narysuj go obok! narysuj wysokość tego trójkąta bo trzeba ja wyliczyć bo potrzebnado pola tak? bo pole tegotrójkąta to P= (1/2) *a * h_ść wylicz h_ść też z tw. Pitagosasa dasz radę bo zobaczysz w tym trójkacie ,że h_śc²= k² - [(1/2)*a]² k= 4 (1/2)*a= 1 policz to h_śc i już będziesz miec pole jednej ściany pole całkowite to P_p + 6* P_ść i tyle Napisz co wyszło !

coco: Coś nie tak w Twoim obliczeniu zobacz: V= (1/3) *6 * 2² *√3 /4 *(2√3) V= 2*2*√3*√3 = 4 *3 = 12 cm ³ bo √3 *√3 = √9 =3

martina: h=√15 P=24+6*√15.... tylko coś czuje,że jeszcze powinnam to rozbić,ale nie wiem jak

martina: aaaaaa.....i już wiem co mi nie wychodziło! czyli P=6(√3+√15?

coco: Tak h= √15 --- jest superrrrr co to za pole w tym poprzednim ? Ostatnie jest ok! P_p= 6√3 p_śc= √15 to P_c = 6√3 +6√15 = 6(√3 +√15) cm ² no widzisz ? proste! rozumiesz to zadanko? Powodzenia przy podobnych !

martina: jejku super tłumaczenie,naprawdę extra! czy jak będę miała jakieś inne problemy mogę dać znać? wiem,że może to zadanie jest banalne... lecz ja jestem typem humanisty

coco: Ok! polecamy się ! jak będziesz mieć problem ? pisz ! Możesz na Nas liczyć! Chętnie pomożemy! Powodzenia!

wioleta:): rury ułożono w warstwach różniących się o 1 rurę. Ułożono w ten sposób 652 rury. Każda o średnicy 60mm. Dolna warstwa zajeła 2,4m. Czy można je ułożyć na jednym stosie? jeżeli tak to ile jest w 3 najwyższych warstwach?

Sz: W ostrosłupie prawidłowym sześciokątnym krawędź podstawy jest równa 2 i jest trzy razy krótsza od krawędzi bocznej. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa. Proszę o pomoc!

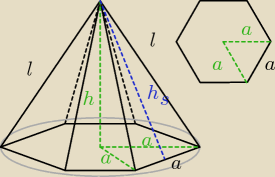
dero2005: oznaczenia: a − długość krawędzi podstawy (ponieważ podstawą jest sześciokąt foremny promień okręgu opisanego jest równy długości boku sześciokąta, jak na rys po prawej u góry) h − wysokość ostrosłupa l − długość krawędzi bocznej h_s − wysokość ściany bocznej z warunków zadania wynika, że a = 2, l = 3a = 3*2 = 6 najpierw obliczamy pole podstawy

	3a2√3		3*22√3
Pp =		=		= 6√3
	2		2

teraz liczymy wysokość ściany bocznej h_s z tw Pitagorasa h_s² + (^a₂)² = l² h_s = √l² − (^a₂)² = √6² − 1² = √35 ponieważ ściany boczne są trójkątami równoramiennymi o podstawie a i wysokości h_s pole boczne liczymy jako pole sześciu takich trójkątów

	a*hs
Pb =		*6 = 3a*hs = 3*2*√35 = 6√35
	2

Pole całkowite jest sumą pola podstawy i pola bocznego P_c = P_p + P_b = 6√3 + 6√35 = 6(√3 + √35) teraz liczymy wysokość h ostrosłupa z tw Pitagorasa h² + a² = l² h² = l² − a² = 6² − 2² = 36 − 4 = 32 h = √32 = 4√2 liczymy objętość ze wzoru

	Pp*h		6√3*4√2
V =		=		= 8√6
	3		3

Asia: krawedz podstawy ostrosłupa prawidłowego szesciokatnego ma dlugosc 4dm,a kat miedzy ściana boczna i płaszczyzna podstawy ma 45.Oblicz objetosc tego ostrosłupa

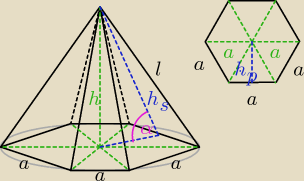
dero2005: α = 45^o a = 4 dm

	a√3		4√3
hp =		=		= 2√3 dm
	2		2

h
	= tg 45o = 1
hp

h = h_p = 2√3 dm

	3
Pp =		√3a2 = 24√3 dm2
	2

V = ¹₃P_p*h = ¹₃*24√3*2√3 = 48 dm³

pattynka: 1.Trzy liczby których suma =49 tworzą ciąg geometryczny. Jeśli do pierwszej liczby dodamy 1 do drugiej 4 a od trzeciej odejmiemy 9 to otrzymamy ciąg arytmetyczny. Wyznacz liczby. 2.Punkty A=(1,3), C=(7,1) są przeciwległymi wierzchołkami kwadratu ABCD. Wyznacz współrzędne pozostałych wierzchołków kwadratu. mogę prosić o rozwiązanie?

bfdgd: hate maths!

SSAS: aha

Magda: jak obliczyć wysokość graniastosłupa pięciokatenego?

Rolcia: Chcę Wam bardzo podziękować, a szczególnie coco. Miałam podobne zadanie i dzięki Tobie udało mi się je rozwiązać.

Eta: 6 lat temu skąd ja to znam ?...... coco = Eta

Eta: Widać już pora na zasłużony odpoczynek Teraz "pałeczkę" przejmie Saizou , Kacper, Godzio , bezendu ............

Eta: