Ostrosłup Magda: Dany jest ostrosłup o wysokości h. W jakiej odległości od wierzchołka należy go przeciąć płaszczyzną równoległą do podstawy, aby podzielić ostrosłup na dwie części o równych objętościach.

Godzio:

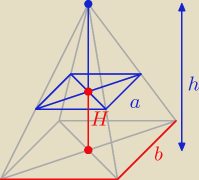
a		h − H		b(h − H)
	=		⇒ ah = b(h − H) ⇒ a =
b		h		h

	H
Vostrosłupa ściętego =		(P1 + P2 + √P1*P2)
	3

Gdzie P₁ i P₂ to pola podstaw, H to wysokość ostrosłupa ściętego

	H		H		b2(h − H)2		b2(h − H)
V =		(b2 + a2 + ab) =		(b2 +		+		)
	3		3		h2		h

	1		1		b2(h − H)3
Vmałego ostrosłupa =		a2 * (h − H) =		*
	3		3		h2

Szukane jest (h − H)

H		b2(h − H)2		b2(h − H)		1		b2(h − H)3
	(b2 +		+		) =		*
3		h2		h		3		h2

	(h − H)2		h − H		(h − H)3
H(1 +		+		) =		/ * h2
	h2		h		h2

H(h² + (h − H)² + h(h − H) ) = (h − H)³ h − H = t ⇒ H = h − t (h − t)(t² + t * h + h²) = t³ h³ − t³ = t³ 2t³ = h³

	h3
t3 =
	2

	h		h3√4
t =		=
	3√2		2

kamilek: dzięki, spróbuje to zrozumieć

Godzio: Dodam, że to co na początku jest wynika z podobieństwa tych ostrosłupów

Godzio: Wiesz co ? Nie patrz na to rozwiązanie bo ja sobie przeczytałem że to jest ostrosłup prawidłowy czworokątny Zaraz Ci napiszę uogólnione

Godzio:

	H
V =		(P1 + P2 + √P1P2)
	3

	1
V1 =		* P2 (h − H)
	3

	P1
Z podobieństwa wynika że		= √hh − H ⇒ P1 = √hh − H * P2
	P2

1		H
	* P2 (h − H) =		(P1 + P2 + √P1P2)
3		3

1		H
	* P2 (h − H) =		(P1 + P2 + √hh − H * P22)
3		3

1		H		3
	* P2 (h − H) =		(P1 + P2 + P2√hh − H) / *
3		3		P2

	P1
h − H = H(		+ 1 + √hh − H)
	P2

h − H = H( √^h_{h − H} + 1 + √^h_{h − H}) / * √h − H (h − H)^3/2 = H(2√h + √h − H) √h − H = t ⇒ H = h − t² t³ = (h − t²)(2√h + t) t³ = 2h√h + ht − 2√ht² − t³ 2t³ + 2√ht² − ht − 2h√h = 0 2t²(t + √h) − h(t + √h) = 0 (t + √h)(2t² − h) = 0 (t + √h)(√2t − √h)(√2t + √h) = 0 i t > 0

	√h		√h
t = −√h − opada lub t =		lub t = −		− odpada
	√2		√2

	√2h
Odp: t =
	2