Wyznaczyc pole obszaru ograniczonego krzywymi
sheel:
y=x
3 y=
3√x
Rozwiązanie musi być za pomocą całki oznaczonej. Potrafie obliczyć całkę ale nie wiem która
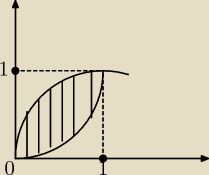
funkcja powinna być odjęta od której. Wykresy funkcji tworzą mniej więcej coś takiego i mamy
obliczyc obszar zakreskowany. czy powinno to być:
a)
3√x−x
3
b)x
3−
3√x
Prosze o odpowiedz i wytłumaczenie
Basia:
ad.1
szukamy punktów przecięcia
x
3 =
3√x /()
3
x
9 = x
x
9−x=0
x(x
8−1)=0
x=0 lub x=1
y=0 lub y=1
A=(0,0)
B(1,1)
P = | ∫
01(
3√x−x
3) dx |
nie musisz wtedy dbać o to co jest "wyżej" a co "niżej", ale tu jest właśnie tak
żeby to stwierdzić wystarczy wybrać dowolną liczbę ∊(0,1) np.
18
i policzyć
f(
18) =
3√18 =
12
| | 1 | | 1 | |
g(18) = (18)3 = |
| < |
| |
| | 83 | | 2 | |
czyli wykres g(x) = x
3 jest "niżej"
