Znajdź punkty przegięcia wykresu funkcji Piotr: Witam wszystkich serdecznie Znajdz punkty przegięcia wykresu funkcji: f(x)=xe^1/x Doszedłem do drugiej pochodnej, a mianowicie:

	e1/x
f"(x)=
	x3

No i teraz oczywiście trzeba przyrównac f" do zera f"(x)=0 (no to jedziemy):

e1/x
	=0 / x3
x3

e^1/x=0 ( no i zonk! ) nie wiem co zrobić podejrzewam że trzeba podzielic przez ln ale nie wiem gdzie to widzialem. Potrzebuje pomocy jak obliczyc miejsce zerowe tej drugiej pochodnej funkcji.

Basia: e^x > 0 dla każdego x∊R czyli e^x≠0 i e^1/x≠0 ale coś mi się ta pochodna nie podoba

Basia:

	−1
f'(x) = 1*e1/x+x*e1/x*		=
	x2

	e1/x
e1/x−		=
	x

e^1/x*[ 1 − ¹_x ]

	−1		1		1
f"(x) = e1/x*		*[1−		] + e1/x*		=
	x2		x		x2

	1		1
e1/x*		*[ −1+		+1 ] =
	x2		x

e1/x
x3

jednak jest dobrze e^1/x≠0 ⇒ f. nie ma punktów przegięcia

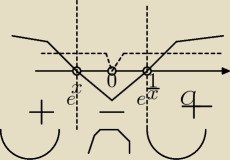
Piotr: czyli tak jak na rysunku

Piotr: aha e^1/x nie ma punktów przegięcia wielkie dzięki Baską cienki z matmy jestem. Rysowałem ten rysunek jak obliczałas pochodną dlatego oświeżyłem ten temat. Wielkie dzięki. Lece walczyc dalej z zadaniami

Basia: nie e^1/x tylko f(x) = x*e^1/x nie ma punktów przegięcia (ale e^1/x też nie ma) a dla x=0 ta funkcja nie jest określona do zbadania przebiegu zmienności trzeba policzyć lim_x→0⁻ x*e^1/x = 0*e^−∞ = 0*0 =0 lim_x→0⁺ x*e^1/x tutaj logarytm chyba nic nie da , raczej reguła de l'Hospitala lim_x→0⁺ x*e^1/x =

	e1/x		+∞
limx→0+		=		=
	1x		+∞

	1   e1/x(− )   x2
limx→0+		=
	1   −   x2

lim_x→0⁺ e^1/x = e^+∞ = +∞