ważne:) deutscher: stojak na plakat ma kształt trójkąta równoramiennego o podstawie 2.4 m i wysokośći 2m.naklejony na stojak plakat ma mieć kształt prostokąta(wpisanego w trójąkąt) jakie wymiary musi miec prostokąt aby powierchnia plakatu zajmowała jak największą część powierchni trójąta? panowie jak to zrobić z góry dzięki za pomoc:

deutscher: ?

Kejti: pytanie do panów, więc panie milczą

deutscher: heh: do Pań również:

deutscher: ?

deutscher: moze ETA ty mi pomozesz

Basia: Rysuję, to potrwa

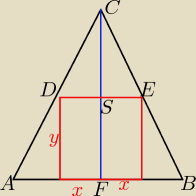
Basia: tr.DSC ~ tr.AFC stąd

DS		DC		SC
	=		=
AF		AC		FC

x		2−y
	=
1,2		2

2x = 1,2(2−y) P=2x*y = 1,2(2−y)*y = −1,2y²+2,4y a ta funkcja osiąga maksimum (bo a= −1,2 <0) dla

	−b		−2,4
y=		=		= 2
	2a		−1,2

a to jest niemożliwe, bo wtedy x=0 gdzieś musi być błąd, albo coś w tym zadaniu jest nie tak

ICSP:

	−Δ
y2 =
	4a

Basia: nie; to jest funkcja zmiennej y z=f(y) = −1,2y²+2,4y czyli taka jak f(x) = −1,2x²+2,4x nie interesuje mnie wartość maksimum pytam dla jakiego argumentu ona to maksimum osiąga

ICSP: 1,2 * 2 = 2,4 a nie 1,2.

ICSP: i wtedy wychodzi że y = 1.

Basia: P=2x*y = 1,2(2−y)*y = (2,4−1,2y)*y = 2,4y − 1,2y² = −1,2y²+2,4y

ICSP: a = −1,2 2a = −2,4 b = 2,4 −b = −2,4

−b		−2,4
	=		= 1. I co dalej?
2a		−2,4

Basia: no i tu jest błąd; nareszcie go znalazłeś

	−b		−2,4
ymax =		=		= 1
	2a		−2,4

x_max = 1,2(2−1) = 1,2 jest to kwadrat o bokach 2x=2,4 i y=2,4 koniec zadania

ICSP: Jakim cudem może być to kwadrat o boku 2,4 skoro bok trójkąta ma 2,4?

ICSP: Według mnie x = 0,6. a y = 1

ICSP: Więc na końcu powstaje prostokąt o bokach. długości x = 1,2 oraz y = 1

Basia: a dobrze; już mi się oznaczenia pomyliły y=1 2x = 1,2(2−1)=1,2 prostokąt ma wymiary: 2x=1,2 y=1 (tak sobie narysowałam, a potem mi się pokiełbasiło; bok to 2x nie x)

ICSP: Teraz można iść w spokoju spać Dobranoc wszystkim.