Wyznacz pole tego trójkąta jako funkcję kąta alfa
Trialking: Dany jest trójkąt równoramienny o ramieniu 4 cm i kącie α przy podstawie. Wyznacz pole
tego trójkąta jako funkcję kąta α. Określ dziedzinę tej funkcji i narysuj jej wykres.
Odczytaj z wykresu, dla jakiego kąta α pole trójkąta jest największe. Bardzo prosze o
pomoc w rozwiązaniu tego zadania

31 sty 19:34
M:
26 lut 16:42
M:
7 lip 16:17
Leszek:
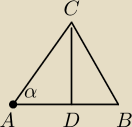
| | AD | |
z ΔADC: cosα = |
| i AC = 4⇒AB = 8cosα |
| | AC | |
| | CD | |
sinα = |
| i CD =h⇒h = 4sinα |
| | AC | |
czyli P
Δ = 8sin2α
P
max dla sin2α =1 ⇒α= π/4
7 lip 20:47
Ryszard: P=1/2*4*4*sin(180−2alfa)=8sin2alfa
Max sin2alfa=1
2alfa=Pi/2
alfa=Pi/4
alfa=45stopni
7 lip 21:24
Ryszard: Dziedzina
P większe od zera
2 alfa należy do zbioru (0,Pi) + 2 k Pi)
czyli:
alfa należy do zbioru:
(0; Pi/2) + k Pi. oraz k należy do zbioru liczb naturalnych
7 lip 22:09
Ryszard: Dodatkowy warunek:
0<2α<π
0<α<π\2 końcowe rozwiązanie
8 lip 12:13
8 lip 14:36

