Udowodnij. Muszyn: Na bokach AB, BC i CA trójkąta ABC zbudowano (na zewnątrz trójkąta) trzy trójkąty równoboczne: AFB, BDC i CEA. Udowodnij, że AD=BE=CF.

Rafael: Po narysowaniu odpowiedniego rysunku(w oparciu o dane z zadania),na mocy twierdzeń kosinusów otrzymasz poniższe zależności: [a²+c²−2cos(α+60^o)]^0,5=[a²+b²−2cos(β+60)]^0,5=CF [b²+c²−2cos(180−{α+β}+60^o)]^0,5=[a²+c²−2cos(α+60^o)]^0,5=BE [b²+c²−2cos(180−{α+β}+60^o)]^0,5=[a²+b²−2cos(β+60^o)]^0,5=AD Teraz dobitnie widać,że CF=BE=CF O rysunek ,ewentualnie prostszy dowód poproś osobiście np:Bogdana

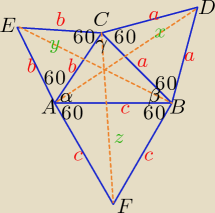
Bogdan: |AD| = x, |BE| = y, |CF| = z. Trójkąty: CFB i ADB są przystające, bo każdy z nich ma bok a, c oraz kąt między tymi bokami w każdym z tych trójkątów ma miarę 60⁰+β, trzecim bokiem w trójkącie CFB jest bok z, trzecim bokiem w trójkącie ADB jest bok x, stąd z = x. Trójkąty: ADC i EBC są przystające, bo każdy z nich ma bok a, b oraz kąt między tymi bokami w każdym z tych trójkątów ma miarę 60⁰+γ, trzecim bokiem w trójkącie ADC jest bok x, trzecim bokiem w trójkącie EBC jest bok y, stąd x = y. Otrzymaliśmy: z = x i x = y, stąd z = y, a więc |AD| = |BE| = |CF|, co należało udowodnić.