liczby zespolone płaszczyzna gaussa
imię lub nick: Zaznaczyć na płaszczyźnie Gaussa zbiór liczb spełniających warunki:
| | ⎧ | |z|2 + Re(z) = 0 | |
| a) | ⎩ | Im(z)≥0 |
|
nie wiem czy dobrze myślę − mam zamienić z na a+bi? i wtedy Re(z)=a Im(z)=b?
25 sty 18:01
imię lub nick:
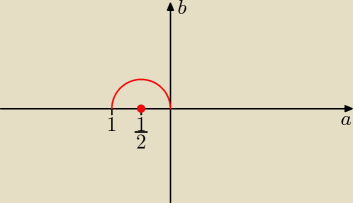

?

a)
|z|
2+Re(z)=0
z=a+bi
|a+bi|
2+a=0
(
√a2+b2)
2+a=0
a
2+b
2+a=0
oraz Im(z)≥0 ⇒b≥0

?

25 sty 18:33
imię lub nick: nikt... nic... ? proszę was, dajcie przynajmniej znak że żyjecie

25 sty 19:03
Trivial: 
25 sty 19:05
imię lub nick: 
a teraz powiedz czy dobrze i jak rozwiązać drugi przykład

25 sty 19:08
Trivial: Masz rację.
25 sty 19:08
Trivial: z = a + bi
z − 1 = a + bi − 1 = (a − 1) + bi
z + 1 = a + bi + 1 = (a + 1) + bi
|z − 1| =
√(a − 1)2 + b2
|z + 1| =
√(a + 1)2 + b2
|z − 1| ≤ |z + 1|
√(a − 1)2 + b2 ≤
√(a + 1)2 + b2
(a − 1)
2 + b
2 ≤ (a + 1)
2 + b
2
(a − 1)
2 ≤ (a + 1)
2
a
2 − 2a + 1 ≤ a
2 + 2a + 1
4a ≥ 0
a ≥ 0
Im(z
2) = 2
Im(a
2 − b
2 +2abi) = 2
2ab = 2
ab = 2
25 sty 19:14
Trivial: chochlik przy końcu
2ab = 2
ab = 1
25 sty 19:14
imię lub nick: heh, świetnie. Ale w tym drugim sprawa się komplikuje:
z rozwiązania nierówności wychodzi:
dla x∊(−1;1> z≥0 ⇒ a+bi≥0 co mam z tym zrobić?
25 sty 19:15
Trivial:
Liczby zespolone nie mają określonego porządku, czyli znak nierówności nie ma prawa bytu.

25 sty 19:17
imię lub nick: aaaaaaha, bo ja to rozwiązałem jak zwykła nierówność z wartością bezwzględną. dzięki za pomoc

25 sty 19:20

 ?
?  a)
|z|2+Re(z)=0
z=a+bi
|a+bi|2+a=0
(√a2+b2)2+a=0
a2+b2+a=0
a)
|z|2+Re(z)=0
z=a+bi
|a+bi|2+a=0
(√a2+b2)2+a=0
a2+b2+a=0
 ?
? 


 a teraz powiedz czy dobrze i jak rozwiązać drugi przykład
a teraz powiedz czy dobrze i jak rozwiązać drugi przykład

