Obliczenie pola figury... Krzysiek: Mam pytanie. Jak obliczyć pole figury ograniczone wykresem y=tgx, osiami OX i OY, oraz linią x=π/2 Bardzo proszę o pomoc z tym zadaniem.

Grześ: Najpierw narysuj rysunek i pokaż dokładnie o jaką część pola chodzi

Krzysiek: kurcze nie wiem jak sie rysuje wykres tutaj, ale chodzi o wykres funkcji tanges, i tą część od 0 do π/2 po prawej stronie.

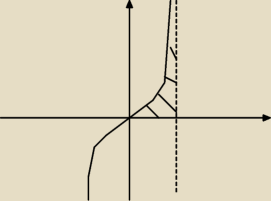
Grześ: Czy chodzi o to zakreskowane pole?

Krzysiek: chodzi o użycie całki tutaj, ale nie mam pojęcia jak to zrobić...

Krzysiek: o właśnie o to mi chodzi

Grześ: Już Ci to zrobię. Chwilkę mi to zajmię Za 5−10 minut. hmm. nie wiem. Cierpliwości

Krzysiek: ok, poczekam, to bardzo ważne dla mnie

Grześ: π/2 ∫ tgx dx = ... 0 Najpierw policzmy całkę nieoznaczoną:

	sinx
∫ tgx dx = ∫		dx =..
	cosx

Podstawienie: t=cosx dt= −sinxdx −dt=sinxdx Czyli:

	1
=.... − ∫		dt = −ln|t|= −ln|cosx|
	t

Wracamy do całki oznaczonej i wprowadzamy małą zmianę: π/2 k ∫ tgx dx = lim k→π/2 ∫ tgx dx = lim k→π/2 [−ln(cosx)]₀^k = 0 0 = lim k→π/2 (−ln(cosk)+ln(cos0)) = lim k→π/2 (−ln(cosk)+ln1) = = lim k→π/2 (−ln(cosk)= +∞ PO obliczeniach wyszło, że ta przestrzeń jest nie do przeliczenia

Grześ: Wiem, dużo pisania, ale dla pewności nawet sprawdzałem w programie do liczenia całek i też pokazał mi, że to pole nie jest ograniczone

Krzysiek:

	1
dzieki wielkie, a taki jeszcze jeden: funkcja jest y=		ograniczona OX prosze o pomoc
	x3

z tym jeszcze

Grześ: http://www.wolframalpha.com/input/?i=int+tg+x+x%3D0..pi%2F2 Taki sam wynik jak mój

Grześ: Ale sprecyzuj to swoje polecenie, bo nie rozumiem o co Ci chodzi..

Krzysiek: chodzi też o obliczenie pola wykresu tej funkcji, to samo co poprzednie

Grześ: ale doprecyzuj swoje polecenie.... Jakie pole Narysuj jakiś szkic chociaż, bo nie będę sie domyślał..

Krzysiek: http://www.speedyshare.com/files/26460230/img1.png i chodzi o pole te zakreskowane.

Grześ: wrzuć na imageshack.us...

Krzysiek: http://img211.imageshack.us/i/img1m.png/

Grześ: Już się za to wezmę... narazie napisz mi jaka jest całka nieoznaczona taka ogólna Czyli policz całke nieoznaczoną

Krzysiek:

	1		1
∫		dx = −		x−2 mam nadzieje że sie nie pomyliłem...?
	x3		2

Grześ: Ta całka oznaczona też nie ma zbieżnego pola. Kurcze.. znowu dużo pisania, a i tak tej całki nie da sie policzyć

Grześ: Dobrze, całka nieoznaczona jest dobrze... To pole też nie jest przeliczalne..

Krzysiek: mógłbyś napisać to rozwiązanie, choć jak mówisz jest to nie do policzenia... bo mi wykładowca łeb urwie jak mu tak powiesz że sie nie da i już

Grześ: Kurcze... szczerze to nie chce mi sie zbytnio tyle pisać... Chciałem poinformować Cię, że ja jestem 2 klasa liceum... tak na marginesie D: Znów zapisz to sobie granicami... Wystarczy w sumie, żę wykażesz dla jednej połówki, bo te pola są sobie równe

Krzysiek: to widze że Ty taki troche bardziej kumaty z tego niż ja, choć młodszy jesteś nieco ode mnie... Jak ma wyglądać taka granica?

Grześ: Policz np. całke oznaczoną od −∞ do 0, czyli: 0

	1		1
∫		dx = lim k→0 [−		]−∞k =
	x3		2x2

−∞ = ... Teraz albo możesz zrobić hmm.. jakos komentarz słowny... nie wiem teraz dokładnie jak to zapisać, ale przy x=0 wartość wyrażenia dąży do nieskończoności. Czyli pole nie zbiega do jakiejś konkretnej wartości...

Krzysiek: dobra, jakoś to wymyśle już. Dzieki wielkie Kolego, szacun dla Ciebie

Grześ: Pozdrawiam serdecznie... pewnie będziesz miał z tego kolosa

Krzysiek: Jutro poprawa z tego... Właśnie tych pól nie ogarniałem, ale myślę że teraz sobie dam rade

Grześ: nie ma sprawy... może miałeś jakieś przykłady, które są przeliczalne Wtedy bym Ci dokładnie pokazał obliczenia jakie ładne wychodzą

Krzysiek: np. dla y=cosx, ogarniczone OX i OY, i linią x=π, ale to już w sumie ogarnąłem.. możesz mi wytłumaczyć jak obliczyć taką całkę:

	dx
∫		umiesz takie cudo zrobić?
	3+4x2

Grześ: umiem

Krzysiek: to możesz się pochwalić

Grześ:

1		1		1
	=		=		=..
3+4x2		4   3(1+ x2)   3		2   3(1+( x)2   √3

	1
Teraz ∫		dx=..
	2   3(1+( x)2   √3

Podstawienie:

	2
t=		x
	√3

	2
dt=		dx
	√3

	√3
dx =		dt
	2

Teraz całka tak wygląda:

	1	√3		1		1
∫			dt = ∫		dt =		arctg t = ...
	3(1+t2)	2		2√3(1+t2)		2√3

Krzysiek: a taka:

	dx
∫
	√2−x2

Grześ: arcsin od razu widzę

Krzysiek: też tak myśle, tylko jak to rozpisać?

Grześ:

1		1		1
	=		=
√2−x2		1   √2(1− x2)   2		1   √2(1−( x)2   √2

	x
Przez podstawienie zrób za t=
	√2

Krzysiek: ma wyjść

√2		x
	arcsin (		) + c
2		√2

Grześ:

	√2
niebardzo.. bez tego
	2

Krzysiek: jak to możliwe?

Krzysiek: ajj, przecież wyłączone 2 też jest pod pierwiastkiem... ok już wiem

Grześ: tak tak Proszę bardzo .. Pozdrawiam serdecznie wykładowcę

Krzysiek: Oj żebyś miał z nim zajęcia... dzieki wielkie, bede sie odzywał jak czegoś ogarniać nie będe. Trzymaj się

Grześ: pisz na gadu 5650170

Krzysiek: ok dzieki

Grześ: napisz mi teraz albo później, żebym wiedział kto pisze

Grześ: hmm