sprawdź czy zachodzi równość Wojtek: tg²(π/5) * tg²(2*π/5)=5

Wojtek:

Wojtek: sprawdź czy zachodzi równość Wojtek: tg2(π/5) * tg2(2*π/5)=5

Eta:

π
	= 36o
5

2π
	= 72o
5

ze wzoru:

	2tgα
tg2α=
	1−tg2α

	2tg18o
tg36o = tg2*18o =
	1−tg218o

tg72^o=ctg18^o , tgα*ctgα=1 => tg18⁰ *ctg18^o= 1

	2tg18o		4
L=(		*ctg18o)2=
	1−tg218o		(1−tg218o)2

	√5−1
sin18o=
	4

to:

	3−√5
sin218o= =
	8

	3−√5		5+√5
cos218o= 1−sin218o = 1−		=
	8		8

	3−√5		8		(3−√5)(5−√5)
to: tg218o=		*		=		=
	8		5+√5		(5+√5)(5−√5)

	20−8√5		2√5
=		=1−
	20		5

	2√5		20		4
(1−tg218o)2= (1−1+		)2=		=
	5		25		5

zatem:

	4
L=		= 5
	45

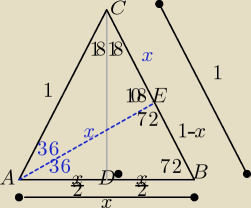
L= P równość zachodzi Wykazuję z rys. ( najprościej)

	√5−1
że : sin18o=
	4

Rysujemy trójkąt równoramienny o ramionach dł. 1 i kątach 72^o, 72^o, 36^o podstawa dł x , x>0,

	x2		x
sin18o =		=
	1		2

ΔABE i ΔAEC mają równe pola bo sin108^o= sin(180^o−72^o)= sin72^o

	x*x
P1=P2=		*sin72o
	2

	x		1−x
zatem:		=
	1		x

x²= 1−x => x²+x −1=0 Δ= 5 √Δ= √5

	−1+√5
x=		v x2 <0 −−− odrzucamy
	2

	x		√5−1
to		=		= sin18o c.n.u
	2		4

P.S. To tylko jeden ze sposobów, może ktoś poda jeszcze inny sposób

Eta: Witam Bogdanie Czekam na prostszy sposób wykazania tej równości .

Eta: @Wojtek Tyle się opisałam....... i co? ....... czekam choć na jedno słowo

Wojtek: Droga Elu dziekuję za rozwiązanie zadania ,mocno ściskam i całuję.Zaglądałem kilkakrotnie ale nie widziałem wczesniej zadnych wpisów.

Trivial: Klawisz F5 może zostać i Twoim przyjacielem!

Eta: Super fajnie Eta .... rozwiązała , a Ela .. dostała całusy

Eta:

Wojtek: Droga Eto Przepraszam za moją ślepotę.

Eta: Nic nie szkodzi, żartowałam

Bogdan: Witaj Eto Zadanie polega na wykazaniu prawdziwości równości: tg²36^o * tg²72^o = 5.

	α		1 − cosα
Korzystam z zależności (dość łatwo ją się wyprowadza) : tg2		=		.
	2		1 + cosα

Zapisujemy naszą równość w takiej postaci:

1 − cos72o		1 + cos36o
	*		= 5 / * (1 + cos72o)(1 − cos36o)
1 + cos72o		1 − cos36o

Po wymnożeniu i redukcji wyrazów podobnych otrzymujemy: 4cos36^ocos72^o + 6(cos36^o − cos72^o) = 4 ⇒ 4cos36^ocos72^o + 6*2sin54^ocos72^o = 4

	sin36o
4cos36ocos72o + 12cos36ocos72o = 4 ⇒ 16cos36ocos72o = 4 / *
	4

4sin36^ocos36^ocos72^o = sin36^o ⇒ 2sin72^ocos72^o = sin36^o sin144^o = sin36^o ⇒ sin36^o = sin36^o, a więc równość jest prawdziwa.